Piston in rigid tube

This problem was worked out by Dr. Hamilton in Acoustics II, while covering waveguides (Ch. 12 of Fundamentals of Physical Acoustics by Blackstock). Note the following differences between my work below and Dr. Hamilton's:

For a treatment of this problem more along the lines of Dr. Hamilton's presentation, see problem 3 of chapter 12 of my physical acoustics quals review webpage.

Contents:

  1. Problem statement
  2. Solution
  3. Sanity checks
  4. Plot of field

Problem statement

Solve the wave equation for the pressure field radiated by a uniform circular velocity source of radius \(a\) positioned with its center on the axis of a rigid cylindrical tube of radius \(b\).

The source conditions at \(z=0\) are \begin{alignat*}{2} u^{(z)} &= u_0 e^{-i\omega t},\quad &&r\in [0,a]\\ u^{(z)} &= 0,\quad &&r\in (a,b] \end{alignat*} and \(\partial p/\partial r = 0\) at \(r=b\) for all \(z\). Note that \begin{equation} \int_0^1 J_m(\alpha'_{mn} x )J_m(\alpha'_{mn'} x) \,x\, dx = \frac{1}{2}[1-(m/\alpha'_{mn})^2] J^2_m(\alpha'_{mn'}) \delta_{nn'} \label{orthogonalityint}\tag{i} \end{equation} is the relevant orthogonality integral (which can be found in J. D. Jackson's Classical Electrodynamics, 1st ed., problem 3.8).

Solution

First of all, there should be no dependence on \(\theta\), because the piston is positioned on-axis. Thus, the azimuthal index \(m\) is set to \(0\).

Since \(\partial p/\partial r = 0\) at \(r=b\), \begin{align*} J'_0(k_r b) = 0 \, \implies \, k_r = \alpha'_{0n}/b\,. \end{align*} Thus, \(k_z = \beta_n = \sqrt{(\omega/c_0)^2- (\alpha'_{0n}/b)^2}\), and the general solution to the wave equation is \begin{equation} \label{general solution}\tag{ii} p(r,z,t) = \sum_{n=1}^\infty A_n J_0(\alpha'_{0n}r/b) e^{i(\beta_n z- \omega t)}\,. \end{equation}

Meanwhile, to satisfy the source condition at \(z = 0\), the momentum equation \(u^{(z)} = (i\omega \rho_0)^{-1}{\partial p}/{\partial z}\) is invoked and set equal to the source condition: \begin{align} \frac{1}{\rho_0 c_0 k}\sum_{n=1}^\infty A_n \beta_n J_0(\alpha'_{0n} r/b) e^{-i{\omega t}}= \begin{cases} u_0 e^{-i\omega t},\quad &r\in [0,a]\\ 0,\quad & r\in (a,b] \end{cases}\,.\tag{iii}\label{sldfkjlkjkljlk} \end{align}

The orthogonality relation given by Eq. \eqref{orthogonalityint} is now used to find the expansion coefficients \(A_n\). Letting \(x = r/b\) and thus \(dx = dr/b\), the orthogonality relation becomes \[\int_0^b J_m(\alpha'_{mn} r/b)J_m(\alpha'_{mn'} r/b) r\, dr = \frac{b^2}{2}[1-(m/\alpha'_{mn})^2] J^2_m(\alpha'_{mn'}) \delta_{nn'}\,,\] which for \(m=0\) reads \begin{equation}\label{orthogonalityint'}\tag{iv} \int_0^b J_0(\alpha'_{0n} r/b)J_0(\alpha'_{0n'} r/b) r\, dr = \frac{b^2}{2} J^2_0(\alpha'_{0n'}) \delta_{nn'} \,. \end{equation} Multiplying both sides of Eq. \eqref{sldfkjlkjkljlk} by \(J_0(\alpha'_{0n'} r/b) r dr\) gives \begin{align*} \frac{1}{\rho_0 c_0 k}\sum_{n=1}^\infty \beta_n A_n J_0(\alpha'_{0n} r/b)J_0(\alpha'_{0n'} r/b) r dr = \begin{cases} u_0 J_0(\alpha'_{0n'} r/b) r dr,\quad &r\in [0,a]\\ 0,\quad & r\in (a,b] \end{cases}\,, \end{align*} where the \(e^{-i\omega t}\) time dependence has been suppressed. Integrating from \(0\) to \(b\) gives \begin{align*} \frac{1}{\rho_0 c_0 k}\sum_{n=1}^\infty \beta_n A_n \int_{0}^{b} J_0(\alpha'_{0n} r/b)J_0(\alpha'_{0n'} r/b) r dr &= u_0 \int_{0}^{a} J_0(\alpha'_{0n'} r/b) r dr\end{align*} Eq. \eqref{orthogonalityint'} is used to integrate the left-hand side, and the recursion relation given by equation (11-A-24c) in Blackstock's book is used to integrate the right-hand side by setting \(v = r/b\) and \(dv = dr/b\): \begin{align*} \frac{b^2}{\rho_0 c_0 k}\sum_{n'=1}^\infty \beta_n A_n \frac{1}{2} J_0^2(\alpha'_{0n'}) \delta_{nn'} &= u_0 ({b}/{\alpha'_{0n'}})^2 v J_1(v)\bigg\rvert_{v=0}^{v=\alpha'_{0n'}a/b}\\ \frac{b^2}{2\rho_0 c_0} \frac{\beta_n}{k} A_n J_0^2(\alpha'_{0n}) &=u_0 \, ab \, \frac{1}{\alpha'_{0n}} J_1(\alpha'_{0n}a/b)\, \end{align*} Solving for \(A_n\) results in \begin{equation}\label{An}\tag{v} A_n = \rho_0 c_0 u_0 \, \frac{a}{b}\, \frac{2k}{\beta_n\alpha'_{0n}}\, \frac{J_1(\alpha'_{0n}a/b)}{J_0^2(\alpha'_{0n}) }\,. \end{equation} Insertion of Eq. \eqref{An} into Eq. \eqref{general solution} results in the solution to the wave equation, \begin{equation}\label{solution}\tag{vi} p(r,z,t) = \rho_0 c_0 u_0\, 2k \, \frac{a}{b} \sum_{n = 1}^\infty \, \frac{1}{\beta_n\alpha'_{0n}}\, \frac{J_1(\alpha'_{0n}a/b)}{J_0^2(\alpha'_{0n}) }\, J_0(\alpha'_{0n}r/b)\, e^{i(\beta_n z- \omega t)}\,, \end{equation} where \(\beta_n = \sqrt{(\omega/c_0)^2- (\alpha'_{0n}/b)^2}\).

I confirmed with Dr. Hamilton that the above solution matches the one presented in class (only with \(a\) and \(b\) flip-flopped, as noted above).

Sanity checks

To check the validity of Eq. \eqref{solution}, several limiting cases are studied.

  1. Does Eq. \eqref{solution} satisfy the radial boundary condition, i.e., does \(\partial p/\partial r\rvert_{r=b}=0\)?

    This is easy to check by differentiating Eq. \eqref{solution} with respect to \(r\), setting \(r=b\), and noting that \(J_0'(\alpha'_{0n}) = 0\). Thus all the terms in the infinite series vanish, and thus the radial boundary condition has been satisfied.

  2. Does Eq. \eqref{solution} recover the velocity source condition?

    To see if the solution recovers the velocity source condition at \(z= 0\), the expansion coefficients given by Eq. \eqref{An} are inserted into into the velocity source condition given by Eq. \eqref{sldfkjlkjkljlk}, and the left- and right-hand-sides are compared. After canceling common terms, one obtains \begin{align} 2 \frac{a}{b}\sum_{n=1}^\infty \frac{1}{\alpha'_{0n}}\, \frac{J_1(\alpha'_{0n}a/b)}{J_0^2(\alpha'_{0n}) } J_0(\alpha'_{0n} r/b) \stackrel{?}{=} \begin{cases} 1,\quad &r\in [0,a]\\ 0,\quad & r\in (a,b] \end{cases}\,. 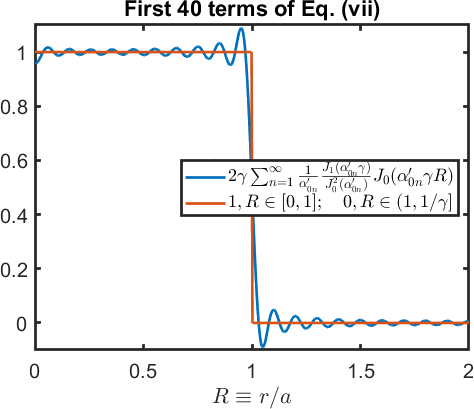\end{align} To check this result, the above equation is nondimensionalized by defining \(\gamma \equiv a/b\) and \(R \equiv r/a\): \begin{align}\label{verifyit}\tag{vii} 2 \gamma \sum_{n=1}^\infty \frac{1}{\alpha'_{0n}}\, \frac{J_1(\alpha'_{0n}\gamma)}{J_0^2(\alpha'_{0n}) } J_0(\alpha'_{0n} \gamma R) \stackrel{?}{=} \begin{cases} 1,\quad & R \in [0,1]\\ 0,\quad & R\in (1,1/\gamma] \end{cases}\,. \end{align}

    See here for my code that shows that the LHS and RHS of Eq. \eqref{verifyit} are equal. The roots of the derivative of the \(0^\mathrm{th}\) order Bessel function are given by a user-defined function by Jack Hallveld (and I verified the first few roots of \(J_0\) by comparing with those listed on page 393 of Fundamentals of Physical Acoustics).

    As an example, for \(\gamma = a/b = 1/2\) and truncation at the first 40 terms in the infinite sum, one obtains

Plot of field

Identify the following dimensionless variables that are conventionally used to nondimensionalize unfocused sound beams: \(P \equiv p/\rho_0c_0u_0\), \(\gamma \equiv a/b\), \(R \equiv r/a\), \(Z \equiv z/z_0\) (where \(z_0 = ka^2/2\) is the Rayleigh distance), \(K \equiv ka\), \(B_n \equiv \beta_n a = \sqrt{K^2 - (\gamma\alpha_{0n}')^2}\), and \(\theta = \omega t\). Then Eq. \eqref{general solution} becomes \begin{equation}\label{virtualsol'}\tag{viii} P(R,Z) = 2K\gamma \sum_{n=1}^{\infty} \frac{1}{B_n \alpha_{0n}'} \frac{J_1(\alpha_{0n}'\gamma)}{J_0^2(\alpha_{0n}')} J_0(\alpha_{0n}'\gamma R)e^{i(KZB_n/2-\theta)}\,. 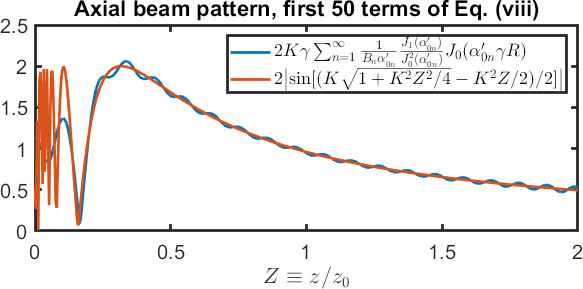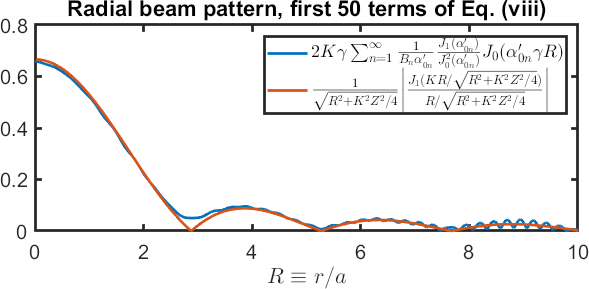\end{equation} Setting \(\gamma = 1/10\) and \(ka = 100\), the magnitude of Eq. \eqref{virtualsol'} at (\(z=z_0\)) is plotted below and compared with the magnitude of the far-field directivity of a uniform circular piston (see problem 13): \[|p(r_\circ,\theta_\circ)| = \rho_0c_0u_0 \frac{ka^2}{2} \frac{1}{r_\circ} \frac{2J_1(ka\sin\theta)}{ka\sin\theta}\,, \] where \(r_\circ\) is the spherical radial coordinate, equal to \(\sqrt{r^2 + z^2}\) in cylindrical coordinates, and where \(\theta_\circ\) is the spherical polar coordinate, and thus \(\sin\theta_\circ = r/\sqrt{r^2 + z^2}\) in cylindrical coordinates. Nondimensionalized, the far-field pressure reads \[|P(R, Z)| = \frac{1}{\sqrt{R^2 + K^2Z^2/4}} \bigg|\frac{J_1(KR/\sqrt{R^2 + K^2Z^2/4})}{R/\sqrt{R^2 + K^2 Z^2/4}}\bigg|\,.\] The plot below is generated at \(z = 1.5 z_0\):

Also plotted is the analytical solution of the Helmholtz equation (see problem 7) for the on-axis pressure magnitude due to a uniform circular piston: \[|p(0,z)| = 2\rho_0c_0 u_0\, \big|\!\sin[k(\sqrt{a^2+z^2}-z)/2]\big| \,. \] Nondimensionalized, the on-axis pressure magnitude reads \[|P(0,Z)| = 2\,\big|\!\sin[(K\sqrt{1+K^2Z^2/4}-K^2Z/2)/2]\big| \,: \]