Physical acoustics

Chapter 1: What is a wave?

What is a wave? [answer]
Rather than providing a direct definition, Blackstock provides six qualities that broadly characterize waves.
1. Waves are disturbances from a pre-existing condition.
2. Waves involve time evolution and travel at finite speeds.
3. For mechanical waves, there exists a medium.
4. Waves are distinct from gross movement of matter.
5. Waves can be idealized by a wave equation.
6. Waves need not be oscillatory.
Points (1), (2), and (6) apply to all types of waves. (3) and (4) only apply to mechanical waves in the continuum approximation and could therefore be excluded for a more general perspective. (5) is debatable.

See also: What is a Wave? by Scales and Snieder.
Derive the d'Alembert solution of the 1D wave equation. [answer]

The general solution to the 1D wave equation is \(\xi(x,t) = f(x-ct)+ g(x+ct)\). Write \begin{align} P(x)&=\xi(x,0)= f(x) + g(x)\label{Pd}\tag{i}\\ Q(x)&=\xi'(x,0)= -cf'(x) + cg'(x)\,.\label{Qd}\tag{ii} \end{align} Integrate equation (\ref{Qd}) and combine with equation (\ref{Pd}) to obtain \begin{align} f(x)&=\frac{1}{2}P(x)- \frac{1}{2c}\int Q(y)dy \tag{iii}\label{df}\\ g(x)&=\frac{1}{2}P(x)+ \frac{1}{2c}\int Q(y)dy\,.\tag{iv}\label{dg} \end{align} Replace \(x\mapsto x-ct\) in equation (\ref{df}) and replace \(x\mapsto x+ct\) in equation (\ref{dg}) and let the lower limit of the integrals be \(x_0\): \begin{align} f(x-ct)&=\frac{1}{2}P(x-ct)- \frac{1}{2c}\int_{x_0}^{x-ct} Q(y)dy \tag{v}\label{df1}\\ g(x+ct)&=\frac{1}{2}P(x+ct)+ \frac{1}{2c}\int_{x_0}^{x+ct} Q(y)dy\,.\tag{vi}\label{dg1} \end{align} Finally, add equations (\ref{df1}) and (\ref{dg1}) to obtain the d'Alembert solution, \begin{equation*} \xi(x,t) = \frac{1}{2}\big\lbrack P(x-ct)+ P(x+ct) \big\rbrack + \frac{1}{2c}\int_{x-ct}^{x+ct} Q(y)dy\,. \end{equation*}
What does the d'Alembert solution say about the dependence of the wave speed on the energy of the initial impulse? [answer]

The d'Alembert solution says that the wave speed is independent of the energy of the initial impulse, a hallmark of linear wave phenomena.
Do Blackstock problems 1B-4 and 1B-5. Are these boundary- or initial-value problems? [answer]

Note that both problems are forced wave problems, which are boundary-value problems (i.e., "What is the solution to the wave equation given a particular boundary condition?"). Thus the d'Alembert solution derived in question (2) above is not of use here, since that is the solution to the initial-value problem (i.e., "What is the solution to the wave equation given an initial displacement and velocity). The distinction between boundary- and initial-value problems is a good one to keep in mind, since basically all problems in acoustics can be categorized this way. For example, problems involving waveguides, horns, and diffraction are usually formulated as boundary-value problems. Meanwhile, problems involving modal responses in enclosures are usually formulated as initial-value problems (though rarely explicitly). When finding the eigenfunctions and eigenfrequencies of enclosure, these are the functions and frequencies that would be excited due to an impulse.

1B-4 and 1B-5 are homework problems, so I cannot post the solution, but I will outline what should be done: In 1B-4, the function corresponding to waves traveling to the left should be tossed out. The argument of the initial condition, \(t\), should simply be replaced with \(t- x/c_0\). In 1B-5, both functions should be kept; the solution is identical to that of 1B-4 except for the presence of an additional term, which is has the argument \(t+x/c_0\).
In an RLC circuit, which of the following is complex-valued: the impedance, the characterstic impedance, or both? [answer]

For lossy lines, \(e\) and \(i\) are no longer in phase, and thus the impedance is complex. However, the characteristic impedance is still \(\sqrt{L/C}\).
In all plane progressive waves, what is the relationship between kinetic and potential energy densities? [answer]

The kinetic and potential energy densities are equal. This is as far as Dr. Hamilton goes, but I think this is true for plane standing waves as well. See here for the proof, for waves on a string (but it's an identical argument for all linear wave phenomena).
In what sense are tsunamis shallow-water waves? What does this assumption imply about the particle velocity \(\vec{u}\)? [answer]

Tsunamis are shallow-water waves in the sense that the wavelength \(\lambda\) is much greater than the depth of the ocean \(h_0\), i.e., \(h_0\ll\lambda\). This means that the particle velocity is purely in the \(x\)-direction, i.e., \(\vec{u} = u\vec{e}_x\).
Assuming no losses, the power of a shallow-water wave is conserved and is given by \(\mathcal{W} = \rho_0 g^{3/2}h_0^{1/2}\xi_\text{rms}^2\), where \(\rho_0\) is the ambient water density, \(g\) is the acceleration due to gravity, \(h_0\) is the ocean depth, and \(\xi\) is the wave variable. What does this mean about the dependence of \(\xi\) on \(h_0\)? [answer]

Since \(\mathcal{W}\) is conserved, and since \(\rho_0 g^{3/2}\) is a constant, \(\xi \propto h_0^{-1/4}\). Thus a large amplification \((h_{0,\text{deep}}/h_{0,\text{shallow}})^{1/4}\) of the wave height is acheived when a tsunami wave approaches the shore.
☸ Derive the wave equation for finite deformations of a string. [answer]

This is a tough derivation. It is worked out here. I also made a video of myself deriving it, because this one is so convoluted: nonlinear wave equation for finite deformations of string.
☸ Do Blackstock problem 1-C5, which is to derive the wave equation for a string with variable density per unit length, \(\rho=\rho(x)\). [answer]

This is another homework problem, so I cannot post the solution here. However, note the error of the sign of the second term in the answer provided in Fundamentals. The correct answer is \[\xi_{xx}+ \frac{\mathcal{T}_x}{\mathcal{T}}\xi_x - \frac{1}{c^2}\xi_{tt}=0\,.\]
Derive the continuity equation in 1D. [answer]

The mass of fluid inside a tube of cross-sectional area \(S\) and length \(\Delta x\) is \(\rho S\Delta x\), and the time derivative of this mass must equal the mass inflow \(+\) the mass outflow, which is \(\rho u S\rvert_{x} -\rho u S\rvert_{x+\Delta x} \). That is, \begin{align*} \frac{\partial}{\partial t}(S\Delta x \rho) &= \rho u S\rvert_{x} -\rho u S\rvert_{x+\Delta x} \\ \frac{\partial \rho}{\partial t} &= -\frac{\partial \rho u}{\partial x} \\\frac{\partial \rho}{\partial t} + \frac{\partial (\rho u)}{\partial x}&=0\,. \end{align*}
Derive the momentum equation in 1D. [answer]

The momentum of fluid inside a tube of cross-sectional area \(S\) and length \(\Delta x\) is \(\rho u S\Delta x\), and the time derivative of this momentum must equal the momentum inflow \(+\) the momentum outflow \(+\) the force on the boundaries, which is \(\rho u^2 S\rvert_{x} -\rho u^2 S\rvert_{x+\Delta x} + PS\rvert_{x} - PS\rvert_{x+\Delta x}\). That is, \begin{align*} \frac{\partial}{\partial t}(S\Delta x u \rho) &= \rho u^2 S\rvert_{x} -\rho u^2 S\rvert_{x+\Delta x} + PS\rvert_{x} - PS\rvert_{x+\Delta x} \\ \frac{\partial (\rho u)}{\partial t} &= -\frac{\partial \rho u^2}{\partial x}-\frac{\partial P}{\partial x} \\ \frac{\partial (\rho u)}{\partial t} + \frac{\partial (\rho u^2)}{\partial x} + \frac{\partial P}{\partial x}&=0\,. \end{align*}
What is the equation of state as a Taylor expansion of \(P(\rho)\)? What assumption lets us write \(P(\rho)\) in the first place? What is the definition of the speed of sound \(c\)? What distinguishes \(c\) from \(c_0\)? What are the parameters \(A\) and \(B\), and what is the significance of the parameter \(B/A\) in nonlinear acoustics? [answer]

Generally, the pressure is given by two other state variables, like density and entropy, i.e., \(P = P(\rho,s)\). But in acoustics, we can get by by assuming that even mildly lossy wave propagation is isentropic, according to Dr. Hamilton:
The lossy linear progressive wave equation does indeed describe isentropic wave propagation under the assumed conditions. Until the attenuation is so strong that one is in the gray area of wave propagation versus diffusion (i.e., for an absorption length on the order of the wavelength), the attenuation is a minor perturbation and it introduces a negligible change in the phase speed relative to that in an ideal fluid.
Therefore, for much of acoustics, the isentropic condition lets us assume pressure is only a function of density, i.e., \(P(\rho)\). Just as for any function of one variable, the Taylor expansion of \(P(\rho)= P(\rho_0+\rho')\) about \(\rho_0\) is \begin{align} P(\rho_0 + \rho') &= p_0 + \frac{dP}{d\rho}\bigg\rvert_{\rho=\rho_0}(\rho-\rho_0) + \frac{1}{2!} \frac{d^2P}{d\rho^2}\bigg\rvert_{\rho=\rho_0}(\rho-\rho_0)^2 + \dots \notag\tag{i}\label{TaylorP} \end{align} where \(P = p_0 + p\), \(P(\rho_0)=p_0\), and \(\rho = \rho_0 + \rho'\). Equation (\ref{TaylorP}) can be written as \begin{align} P(\rho_0 + \rho') &= p_0 + \bigg(\rho_0\frac{dP}{d\rho}\bigg)\bigg\rvert_{\rho=\rho_0}\bigg(\frac{\rho-\rho_0}{\rho_0}\bigg) + \bigg(\rho_0^2\frac{1}{2!} \frac{d^2P}{d\rho^2}\bigg)\bigg\rvert_{\rho=\rho_0}\bigg(\frac{\rho-\rho_0}{\rho_0}\bigg)^2 + \dots \notag\\ &= p_0 + A\frac{\rho-\rho_0}{\rho_0} + \frac{B}{2!}\bigg(\frac{\rho-\rho_0}{\rho_0}\bigg)^2 + \dots \tag{ii}\label{TaylorP2} \end{align} where \begin{align*} A&= \rho_0\frac{dP}{d\rho}\bigg\rvert_{\rho=\rho_0} = \rho_0 c_0^2\\ B&=\rho_0^2 \frac{d^2P}{d\rho^2}\bigg\rvert_{\rho=\rho_0}\,, \end{align*} where the definition of the linear speed of sound \(c_0 \equiv (dP/d\rho)\rvert_{\rho=\rho_0}\) has been used. (On the other hand \(c = dP/d\rho\) i.e., not evaluated at at equilibrium density, is the nonlinear speed of sound). Equation (\ref{TaylorP2}) can be rearranged by writing \(P = p_0 + p\) and \(\rho-\rho_0 = \rho'\), and by factoring out \(A\), resulting in Blackstock's equation (C-44): \begin{equation*} p = c_0^2\rho'\bigg( 1 + \frac{B}{2!A}\frac{\rho'}{\rho_0} + \dots\bigg) \end{equation*}
Thus the ratio \(B/A\) is seen to be the coefficient of the first nonlinear term of the isentropic equation of state.
Derive the adiabatic and isothermal sound speeds. For the adiabatic sound speed, use the ideal gas law \(P = \rho R T\) to write the sound speed in terms of the temperature. Who first calculated calculated the adiabatic sound speed? Who first calculated calculated the isothermal sound speed? Which came first? Bonus: Show that \(c_0 = (\gamma/3)^{1/2} v_\text{rms}\), where \(v_{rms}\) is the square root of the mean square velocity of the molecules in the gas. To do so, use the ideal gas law in terms of the Boltzmann constant \(k\) and number of molecules \(N\), \(PV= NkT\) to write the adiabatic sound speed. Note that \(\rho V\) is the mass of the gas, which is equal to \(Nm\), where \(m\) is the molecular weight. Use the equipartition theorem \(kT = \frac{1}{3} m \langle v^2\rangle\) to relate the speed of sound to the average speed of the molecules. [answer]

Recall the adiabatic gas law, \(P = p_0(\rho/\rho_0)^\gamma\). By the definition of linear sound speed, \begin{align*} c_0^2 &=\frac{dP}{d\rho}\bigg\rvert_{\rho=\rho_0}\\ &=\gamma \frac{p_0}{\rho_0} \bigg(\frac{\rho}{\rho_0}\bigg)^{\gamma-1}\bigg\rvert_{\rho=\rho_0}\\ &= \frac{\gamma p_0}{\rho_0}\\ \implies c_0 &= \sqrt{\frac{\gamma p_0}{\rho_0}} = \sqrt{\gamma R T_0}\,, \end{align*} where the second equality in the last line follows from the ideal gas law. This was shown by Laplace.

Next recall the isothermal gas law, \(p/p_0 = \rho/\rho_0\) and repeat the procedure above, giving \[c_0 = \sqrt{p_0/\rho_0}\,.\] One could equivalently set \(\gamma = 1\) in the adiabatic sound speed to recover the isothermal sound speed. Newton had calculated the isothermal sound speed more than a century prior to Laplace's calculation of the adiabatic sound speed.

Bonus: Use the alternate form of the ideal gas law, in terms of number of molecules and the Boltzmann constant: \begin{align*} c_0^2&= \frac{\gamma P_0}{\rho_0}\\ &= \frac{\gamma P_0 V_0}{\rho_0 V_0}\\ &= \frac{\gamma NkT_0}{Nm} \end{align*} Noting that \(kT = \frac{1}{3}m\langle v^2\rangle\), the above becomes \begin{align*} c_0^2 &= \frac{\gamma N m \langle v^2\rangle}{3Nm}\\ &= \frac{\gamma}{3}\langle v^2\rangle \end{align*} Take the square root and note that \(v_\text{rms} = \sqrt{\langle v^2\rangle}\). Thus \begin{align*} c_0 &= (\gamma/3)^{1/2} v_\text{rms} \end{align*} Where does \(kT = \frac{1}{3}m\langle v^2\rangle\) come from? It comes from the equipartition theorem, which says that each quadratic degree of freedom contributes \(kT/2\) to the energy. There are three degrees of freedom for a monatomic gas. Thus \(3kT/2 = \frac{1}{2}m\langle v^2\rangle \), which gives the result. From R. P. Feynman's lecture on the topic,
The speed of sound is of the same order of magnitude as the speed of the molecules, and is actually somewhat less than this average speed. Of course we could expect such a result, because a disturbance like a change in pressure is, after all, propagated by the motion of the molecules.
Derive the linear wave equation in 1D for an isentropic fluid. [answer]

The continuity and momentum equations are linearized, and the linearized state relation \(\rho' = p/c_0^2\) is invoked to eliminate density, resulting in \begin{align} \frac{1}{c_0^2}\frac{\partial p}{\partial t} + \rho_0 \frac{\partial u}{\partial x} = 0\tag{i}\label{linc}\\ \frac{\partial p}{\partial x} + \rho_0 \frac{\partial u}{\partial t} = 0\,.\tag{ii}\label{linm} \end{align} The time derivative of equation (\ref{linc}) and the spatial derivative of equation (\ref{linm}) are taken, and the resulting equations are subtracted, giving the wave equation, \[\frac{\partial^2 p}{\partial x^2} - \frac{1}{c_0^2}\frac{\partial^2 p}{\partial t^2}=0\,.\]
Derive the plane wave impedance relation for linear 1D sound in air. How does the answer change as the direction of the sound reverses? [answer]

Let \(p = f(x-c_0t)\). Then by the momentum equation \(\rho_0 \partial u/\partial t= -\partial p/\partial x\), \begin{align*} u &= -\frac{1}{\rho_0}\int f'(x-c_0t)dt\\ &= -\frac{1}{\rho_0}\bigg(-\frac{1}{c_0}\bigg) f\\ &= \frac{1}{\rho_0 c_0}p\\ \implies \frac{p}{u}&= \rho_0 c_0 \end{align*} If the direction of the sound is reversed, \(p = f(x+c_0t)\), which results in \(p/u= -\rho_0 c_0\).
Derive the spherical wave impedance relation for linear outgoing spherical sound. Write the impedance in polar and rectangular form. How does this impedance change for converging spherical waves? [answer]

Consider the imaginary part of a solution of the spherically symmetric wave equation, \begin{equation}\label{impart} p = \frac{\Im e^{j(\omega t-kr)}}{r}\,.\tag{i} \end{equation} Equation (\ref{impart}) is inserted into the radial component of the momentum equation, where \(\partial u/\partial t =j\omega u\) \begin{align} j\omega \rho_0 u &= -\frac{\partial p}{\partial r}\notag\\ u&= \frac{1}{j\omega \rho_0}\bigg(jk + \frac{1}{r}\bigg) p\notag\\ \implies \frac{p}{u} &= \frac{j\omega \rho_0}{jk + 1/r}\notag\\ \frac{p}{u} &= \frac{j\omega \rho_0/jk}{1 + 1/jkr}\notag\\ Z= \frac{p}{u} &= \frac{\rho_0 c_0}{1 + 1/jkr}\tag{ii}\label{impers}\,. \end{align} The rectangular and polar forms of equation (\ref{impers}) are \begin{align*} Z &= \frac{\rho_0 c_0}{1+1/k^2 r^2} + j\frac{\rho_0c_0/kr}{1+1/k^2 r^2}\\ &= \rho_0 c_0 \frac{kr}{\sqrt{1+k^2r^2}} e^{j\text{arccot} kr}\,. \end{align*} For incoming spherical waves \(p = \frac{\Im e^{j(\omega t+kr)}}{r}\), equation (\ref{impers}) obtains two additional negative signs: \begin{align*} j\omega \rho_0 u &= -\frac{\partial p}{\partial r}\notag\\ u&= \frac{1}{j\omega \rho_0}\bigg(-jk + \frac{1}{r}\bigg) p\notag\\ \implies \frac{p}{u} &= \frac{j\omega \rho_0}{-jk + 1/r}\notag\\ \frac{p}{u} &= \frac{-j\omega \rho_0/jk}{1 - 1/jkr}\notag\\ \frac{p}{u} &= -\frac{\rho_0 c_0}{1 - 1/jkr}\,. \end{align*}
Interpret the \(kr\ll 1\) and \(kr\gg 1\) limits of the spherical wave impedance relation. What limit represents efficient radiation? [answer]

From the above problem, the rectangular form of equation (\ref{impers}) is \begin{align*} Z = \frac{\rho_0 c_0}{1+1/k^2 r^2} + j\frac{\rho_0c_0/kr}{1+1/k^2 r^2}\,, \end{align*} from which it can be seen that for \begin{align*} Z = \begin{cases} \rho_0 c_0 &\text{for}\quad kr\gg 1\\ j\omega\rho_0 r &\text{for}\quad kr\ll 1 \end{cases} \end{align*} The \(kr \gg 1\) limit represents efficient radiation, as the impedance is purely real and recovers the plane wave impedance relation. Meanwhile the \(kr \ll 1\) limit is purely reactive, representing poor radiation.
Calculate the pressure field due to a pulsating sphere of radius \(a\), where the particle velocity is \(u_0 e^{j\omega t}\). [answer]

We know the solution must have the form \begin{equation}\label{formofsol}\tag{i} p(r,t) = \frac{A}{r}\exp{j(\omega t - kr)}\,. \end{equation} To determine the constant \(A\), recall the spherical wave impedance relation, \begin{align*} Z(r=a) = \frac{p(r=a)}{u(r=a)}=\frac{\rho_0 c_0}{1+1/jka}\,, \end{align*} and match the boundary condition \(u_0 e^{j\omega t}\) at the radius \(a\) to the pressure at \(r=a\): \begin{align}\label{ata}\tag{ii} p(r=a,t) = u_0 e^{j\omega t}\frac{\rho_0 c_0}{1+1/jka} \end{align} Setting equations (\ref{formofsol}) and (\ref{ata}) equal gives \begin{align} \frac{A}{a}\exp{j(\omega t - ka)} &= u_0 e^{j\omega t}\frac{\rho_0 c_0}{1+1/jka}\notag\\ \implies A&= \frac{\rho_0 c_0 u_0 a}{1+1/jka}\exp{jka}\label{Aeq}\tag{iii} \end{align} The pressure field is therefore given by combining equations (\ref{formofsol}) and (\ref{Aeq}): \begin{align*} p(r,t) = \frac{\rho_0 c_0 u_0}{1+1/jka}\frac{a}{r}\exp{j[\omega t- k(r-a)]}\,. \end{align*}
Derive the expression for the instantaneous intensity \(\vec{I}\) of a linear sound wave. [answer]

Two approaches are provided, the second being more formal than the first.

Informal approach. Denoting \(W =\) power = \(dw/dt\), where \(w\) is work, the magnitude of the instantaneous intensity \(I\) is equal to the power \(W\) divided by the surface area \(S\) \begin{align*} I&= {W}/{S} \\ &= \frac{dw}{dt}\frac{1}{S}\\ &= \frac{F\,dx}{S}\frac{1}{dt}\\ &= \frac{F}{S}\frac{dx}{dt}\\ & = p u \end{align*} This quick approach does not retain the vectorial nature of the intensity vector. The formal approach below is therefore preferred.

Formal approach. Define the power \(W\) to be the time derivative of the work \(w\) done by the sound wave: \[W = \frac{dw}{dt}\,.\] Note that the differential work done is \(dw = \vec{F}\cdot d\vec{s}\). Thus \[W = \frac{d}{dt}(\vec{F}\cdot d\vec{s}) = \frac{d\vec{F}}{dt} \cdot d\vec{s} + \vec{F} \cdot \frac{d\vec{s}}{dt}\] The first term, \( \frac{d\vec{F}}{dt} \cdot d\vec{s}\), is infinitesimally small. And \(\frac{d\vec{s}}{dt} = \vec{u}\). Thus \[W = \vec{F} \cdot \vec{u}\] Next consider an area \(S\) with inward unit normal \(\vec{n}\), and suppose that \(\vec{F} = F\vec{n}\). Then, the power can be written as \[W = F\vec{n} \cdot \vec{u} \frac{1}{S} \oint dS\] Assuming \(F\) and \(u\) are constant along the surface, they can be moved inside the integral: \[W = \frac{1}{S} \oint F\vec{n} \cdot \vec{u} dS = \oint (F\vec{n}/S) \cdot \vec{u} dS\] Then identifying \(F\vec{n}/S\) to be the acoustic pressure times the normal vector \(p\vec{n}\) yields \[W = \oint p \vec{u}\cdot \vec{n} dS\] The integrand \(p \vec{u}\) is therefore identified to be the instantaneous intensity vector: \[\vec{I} = p \vec{u}\]
Show that the time-averaged magnitude of the intensity of a plane wave is \(\langle I \rangle = p_\text{rms}^2/\rho_0 c_0 \). [answer]

From the previous problem, the time-averaged intensity is given by \begin{align*} \langle I\rangle &= \langle pu \rangle\\ &= \frac{1}{\rho_0 c_0}\langle p^2 \rangle\\ &=\frac{1}{\rho_0 c_0}\int_{0}^{t_\text{av}}p^2 dt\\ &=\frac{p_\text{rms}^2}{\rho_0 c_0} \end{align*} where the root-mean-square of the pressure is defined as \[p_\text{rms} = \sqrt{\int_{0}^{t_\text{av}}p^2 dt}\]
Calculate the time-averaged intensity due to a spherically symemtric outgoing wave, \(p = \frac{A}{r}\exp{j(\omega t - kr)}\). What about this result is often misquoted? [answer]

The time-avereraged intensity is given by \begin{align*} \langle I \rangle &= \langle pu \rangle\\ &= \frac{1}{2}\Re(pu^*)\\ &=\frac{1}{2\rho_0c_0}\Re(pp^*(1+1/jkr))\\ &=\frac{1}{\rho_0c_0}\frac{|p|^2}{2}\\ &=\frac{p_\text{rms}^2}{\rho_0 c_0} \end{align*}
Find \(p_\text{rms}\) for a sinusoidal wave and for an N-wave, both of amplitude \(A\). [answer]

By taking the integral \(p_\text{rms}^2 = \frac{1}{t_\text{av}}\int_0^{t_\text{av}} p^2 dt\), one finds that \(p_\text{rms} = A/\sqrt 2\) for a sinusoidal wave and \(p_\text{rms} = A/\sqrt 3\) for N-waves.
State the definitions of the sound pressure level (\(\text{SPL}\)), intensity level (\(\text{IL}\)), and sound power level (\(\text{PWL}\)). What is the \(\text{IL}\) in a purely standing wave field? [answer]

The definitions are \begin{align*} \text{SPL}&=20 \log_{10} (p_\text{rms}/p_\text{ref})\\ \text{IL}&=10 \log_{10} (\langle I\rangle/I_\text{ref})\\ \text{PWL}&=10 \log_{10} (W/W_\text{ref})\,, \end{align*} where Blackstock writes "\(I\)" for the time-averaged intensity vector instead of \(\langle I \rangle\). SPL and IL are functions of distance from a sound source (because, e.g., sound pressure is proportional to \(1/r\) and intensity is proportional to \(1/r^2\) in a spherical wave) whereas PWL is the total power radiated by a sound source, wherever it goes and however it diverges. The \(\text{IL}\) in a purely standing wave field is \(-\infty\), because \(I = 0\).

It is a good thing to be able to show that \(\langle I\rangle = 0\) in a standing wave field. Consider the standing wave \(p(x) = A\cos(kx)\). Then by the momentum equation, \[u = \frac{jka}{\rho_0}\int \cos kx dt = \frac{jkA}{\rho_0}(t-\phi)\cos{kx},\] where \(\phi\) is a phase. Then the time-averaged intensity is given by (see problem 28 for the derivation of the first line below) \begin{align*} \langle I \rangle &= \frac{1}{2} \Re (pu^*)\\ &= \frac{1}{2}\Re{\bigg(j\frac{kA^2}{\rho}(t-\phi)\cos^2{kx} \bigg)}\\ &=0\,. \end{align*}
☸ Calculate the energy density of linear sound. What is the relationship between kinetic and potential energy densities in a progressive plane wave? State and derive the acoustic energy corollary. [answer]

This is another hard one. See here, or here for a video (The video includes the derivation of the acoustic energy corollary). I doubt we are responsible for these kinds of clever manipulations, but it's good to know the main result, that the kinetic and potentitial energy densities are equal in a progressive plane wave. The potential and kinetic energies being equal for progressive waves recovers a special case of the virial theorem.
What is the difference between acoustic, specific acoustic, and mechanical impedance? [answer]

The definitions are \begin{align*} Z_\text{sp ac} &= \frac{p}{u}\\ Z_\text{ac} &= \frac{p}{q} = \frac{p}{Su} = Z_\text{sp ac}/S\\ Z_\text{mech} &= \frac{F}{u} = \frac{Sp}{u} = Z_\text{sp ac}S\,. \end{align*}
For plane progressive waves in air, why is the intensity level (\(\text{IL}\)) roughly numerically equal to the sound pressure level (\(\text{SPL}\))? [answer]

The intensity level can be expressed as \begin{align*} \text{IL} &= 10 \log_{10} \frac{\langle I \rangle}{I_\text{ref}}\\ &= 10 \log_{10} \frac{p^2_{\text{rms}}/\rho_0c_0}{I_\text{ref}}\\ &= 10 \log_{10} \frac{p^2_{\text{rms}}}{p^2_{\text{ref}}}\frac{p^2_{\text{ref}}}{\rho_0c_0I_\text{ref}}\\ &= 10 \log_{10} \frac{p^2_{\text{rms}}}{p^2_{\text{ref}}} + 10\log_{10}\frac{p^2_{\text{ref}}}{\rho_0c_0I_\text{ref}}\\ &= 20 \log_{10} \frac{p_{\text{rms}}}{p_{\text{ref}}} + 10\log_{10}\frac{p^2_{\text{ref}}}{\rho_0c_0I_\text{ref}}\\ &\simeq \text{SPL}\, \end{align*}
It turns out that in air at STP the term \(10\log_{10}\frac{p^2_{\text{ref}}}{\rho_0c_0I_\text{ref}}\) is small, like \(-0.16 \)
☸ Consider two time-harmonic functions \(f(t) = Fe^{j(\omega t + \phi_F)} = \tilde{F} e^{j\omega t}\) and \(g(t) = Ge^{j(\omega t + \phi_G)} = \tilde{G} e^{j\omega t}\) (where \(\tilde{F} = Fe^{j\phi_F}\) and \(\tilde{G} = Ge^{j\phi_G}\)). Show that \(\langle \Re (f) \,\,\Re (g) \rangle = \frac{1}{2} \Re (\tilde{F}\tilde{G}^*) = \frac{1}{2} \Re (\tilde{F}^*\tilde{G})\), where "\(\Re\)" denotes "real part". Therefore show that \(\langle \vec{I}\rangle = \langle p \vec{u} \rangle = \frac{1}{2} \Re(p\vec{u}^*) = \frac{1}{2} \Re(p^*\vec{u})\). [answer]

See here for the solution. Letting \(\Re{f} = p\) and \(\Re(\vec{g})= \vec{u}\) immediately leads to \(\langle I\rangle = \frac{1}{2} \Re(p\vec{u}^*) = \frac{1}{2} \Re(p^*\vec{u})\).
Evaluate the integral for time-averaged intensity in Fundamentals of Physical Acoustics, Sec. 1E-3 (page 50), and thereby recover the result above. [answer]

See here for the evaluation, noting that Blackstock suppresses the angle brackets to denote time average, i.e., his \(\vec{I}\) is our \(\langle\vec{I}\rangle\).

Chapter 2: Detailed development of the acoustic wave equation

See An Introduction to Thermal Physics by Daniel Schroeder for more on thermodyanmics.

To what particle does the "particle velocity" \(\vec{u}\) refer? [answer]

"Particle velocity" does not refer to a single molecule. Rather, it refers to a "fluid particle" within the continuum approximation, "a large enough collection of molecules that the average of their random motions is zero," as Blackstock writes (see page 27-28).
Write the exact mass and momentum equations in integral form. [answer]

The conservation of mass in integral form is \[\frac{\partial}{\partial t} \int_\mathcal{V} \rho\, dV + \oint_\mathcal{S} \rho \vec{u} \cdot dS \,= 0\,,\] while the conservation of momentum in integral form is \[\frac{\partial}{\partial t} \int_\mathcal{V} \rho \vec{u}\, dV = \int_\mathcal{V} \vec{B} \rho \,dV - \oint_\mathcal{S} P d\vec{S} - \oint_\mathcal{S} (\rho \vec{u})\vec{u} \cdot d\vec{S} \,.\]
State the 0th, 1st, 2nd, and 3rd laws of thermodynamics. [answer]

Zeroth law: the transitive property. If A is in thermal equilibrium with B, and B is in thermal equilibrium with C, then A is in thermal equilibrium with C.

First law: the conservation of energy. The change in internal energy is the heat plus the work done on the system: \(\Delta U = Q +W\).

Second law: entropy. The entropy of the universe tends towards a maximum, i.e., \(dS \geq \delta Q/T\), where the equality is fulfilled by quasistatic processes.

Third law: absolute zero. The entropy approaches a constant in the limit that the temperature goes to absolute zero.
How many quadratic degrees of freedom \(f\) does helium have? Oxygen? Nitrogen? Bonus: What are the seven diatomic gases? [answer]

Note that quadratic degrees of freedom include translational, rotational, and vibrational types of energies, which are quadratic in velocity, angular velocity, and displacement respectively. Helium is monotomic and therefore has only three translational degrees of freedom: \(f=3\). Oxygen and nitrogen are both diatomic and thus have three translational degrees of freedom and two rotational degrees of freedom: \(f=5\).

The seven diatomic gases can be remembered with the expression, "BrINClHOF!", which indicates that bromine, iodine, nitrogen, chlorine, hyrogen, oxygen, and fluorine are diatomic gases.
State the equipartition theorem. [answer]

The equipartition theorem states that the average energy of any quadratic degree of freedom is \(\frac{1}{2} kT\), where \(k\) is the Boltzmann constant. For example, a system of \(N\) molecules, each with \(f\) degrees of freedom, has a total thermal energy of \(U = N f kT/2\).

Note that for three dimensional motion for a monotomic gas, \(U = 3kT/2\) by the equipartition theorem. As all the energy is kinetic, \(U = m\langle v^2\rangle/2\), where \(\langle v^2\rangle\) is the average of the square of the velocities. Therefore, \(\sqrt{\langle v^2\rangle} = 3kT/m = v_\text{rms}\).
Derive the adiabatic gas law. [answer]

Start with the first law of thermodynamics, and note that the no heat is flows into or out of the gas in an adiabatic process: \[\Delta U = Q+W = W.\] By the equipartition theorem, \begin{align*} U &= \frac{f}{2}NkT\\ \implies dU &= \frac{f}{2}Nk\, dT\,. \end{align*} Setting the above relation equal to the infinitesimal work done by the gas during a compression (because \(dU =dW\)) results in \begin{align*} \frac{f}{2}Nk\, dT &= -P dV \,. \end{align*} Substitution of the ideal gas law \(P = NkT/V\) on the right-hand side and rearrangement gives \begin{align*} \frac{f}{2}\frac{dT}{T} &= -\frac{dV}{V} \,. \end{align*} Integration gives \begin{align*} \frac{f}{2} \ln T/T_0 &= -\ln V/V_0\\ \ln [(T/T_0)^{f/2}] &= -\ln V/V_0 \end{align*} Exponentiation and rearrangement gives \begin{align*} V T^{f/2} &= V_0 T_0^{f/2} \,. \end{align*} Invoking the ideal gas law to eliminate temperature gives \begin{align*} P^{f/2} V^{\frac{f+2}{2}} &= P^{f/2}_0 V^{\frac{f+2}{2}}_0 \,. \end{align*} Raising both sides to the power of \(2/f\) gives \begin{align*} P V^{\frac{f+2}{f}} &= P_0 V^{\frac{f+2}{2}}_0\,. \end{align*} Identifying \(\gamma \equiv (f+2)/f\), and noting that \(V \propto 1/\rho\), gives the desired result: \begin{align*} P \rho_0^{\gamma} &= P^{f/2}_0 \rho^{\gamma}\\ P/P_0 &= (\rho/\rho_0)^{\gamma} \end{align*}
Calculate the work done in an adiabatic compression. [answer]

For an adiabatic compression, \(P = P_0 (V_0/V)^\gamma\), as derived above. The work done on the gas is \begin{align*} W &= -\int_{V_0}^{V_1} P dV\\ &= -\int_{V_0}^{V_1} P_0 (V_0/V)^\gamma dV \\ &= -P_0 V_0^\gamma \int_{V_0}^{V_1} V^{-\gamma} dV\\ &= -\frac{P_0 V_0^\gamma}{1-\gamma}V^{1-\gamma}\bigg\rvert_{V_0}^{V_1} \\ &= -\frac{P_0 V_0^\gamma}{1-\gamma}(V_0^{1-\gamma}-V_1^{1-\gamma})\\ &= \frac{P_0 V_0}{\gamma-1}[(V_1/V_0)^{1-\gamma} - 1]\\ &= \frac{P_0 V_0}{\gamma-1}[(V_0/V_1)^{\gamma-1} - 1] \end{align*}
Is every adiabatic process isentropic? Is every isentropic process adiabatic? [answer]

Every adiabatic process is not isentropic, but every isentropic process is adiabatic. This is because an isentropic process is defined to be a reversible adiabatic process.

Also note that every reversible process is quasistatic, but not every quasistatic process is reversible "if there is also heat flowing in or out or if entropy is being created in some other way" (Schroeder).
Use the entropy equation [see Blackstock equation (2-A-43), or the beginning of Nonlinear Acoustics by Hamilton and Blackstock, or Fluid Mechanics by Lifshitz and Landau], \begin{equation}\label{entropers}\tag{1} \rho T \frac{\partial s}{\partial t}= \kappa \nabla^2 T + \text{miscellaneous terms}\,, \end{equation} to show that low-frequency sound is isentropic, while high-frequency sound is isothermal. [answer]

The thermodynamic quantities in equation (\ref{entropers}) are first expressed as ambient \(+\) perturbation quantities, i.e., \begin{align*} T &= T_0 + T'\\ s &= s_0 + s,. \end{align*} Thus equation (\ref{entropers}) becomes \[\rho_0 T_0 \frac{\partial s'}{\partial t} \sim \kappa \nabla^2 T'\,, \] or, assuming time-harmonic solutions (i.e.,\(\partial/\partial t \mapsto j\omega \) and \(\nabla^2 \mapsto k^2 = \omega^2/c^2\)), \[j\omega\rho_0 T_0 s' \sim \kappa \frac{\omega^2}{c_0^2} T'\,. \] Rearranging this result gives \[\rho_0 c_0^2 \frac{T_0}{\kappa} \frac{s'}{T'} \sim \omega \,,\] from which it can be seen that \begin{align*} s'&\to 0 \quad \text{ as } \quad \omega \to 0,\quad \text{(Isentropic)}\\ T'&\to 0 \quad\text{ as }\quad \omega \to \infty,\quad \text{(Isothermal)}\,. \end{align*} Feynman provides some insightful commentary:
Newton was the first to calculate the rate of change of pressure with density, and he supposed that the temperature remained unchanged. He argued that the heat was conducted from one region to the other so rapidly that the temperature could not rise or fall. This argument gives the isothermal speed of sound, and it is wrong. The correct deduction was given later by Laplace, who put forward the opposite idea—that the pressure and temperature change adiabatically in a sound wave. The heat flow from the compressed region to the rarefied region is negligible so long as the wavelength is long compared with the mean free path. Under this condition the slight amount of heat flow in a sound wave does not affect the speed, although it gives a small absorption of the sound energy. We can expect correctly that this absorption increases as the wavelength approaches the mean free path, but these wavelengths are smaller by factors of about a million than the wavelengths of audible sound.
What is the meaning of \(D/Dt\)? [answer]

This is the material derivative, defined by \[\frac{\partial}{\partial t} + \vec{u}\cdot \gradient\,.\]
☸ Explain the meaning of each term in \begin{align} \frac{D\rho}{Dt} + \rho \gradient\cdot \vec{u} &=0 \label{blacksters1}\tag{i}\\ \rho \frac{D\vec{u}}{Dt} + \gradient P &= (\lambda + 2\mu) \gradient(\gradient\cdot \vec{u}) - \mu \gradient \times \gradient \times \vec{u}\label{blacksters2}\tag{ii}\\ \rho C_v \frac{DT}{Dt} + P \gradient\cdot \vec{u} &= \Phi^{\text{(visc)}} + \kappa \nabla^2 T \label{blacksters3}\tag{iii}\\ P &= R\rho T\,, \label{blacksters4}\tag{iv} \end{align} which correspond to Blackstock's eqs. A-47 - A-49. [answer]

All four of the equations above are exact, i.e., \(\rho\), \(P\), and \(T\) are the exact density, pressure, and temperature. Equation (\ref{blacksters1}) is the continuity equation. Abandoning the material derivative, it is written \[\frac{\partial \rho}{\partial t} + \gradient\cdot (\rho \vec{u}) = 0\,.\] Equation (\ref{blacksters2}) is the momentum equation. \(\lambda \) is the dilatational viscosity coefficient, and \(\mu\) is the shear viscosity coefficient. (Sometimes the two are combined as \(\nabla + 2\mu = \tilde{V}\), where \(\tilde{V}\) is the viscosity number). Abandoning the material derivative, this equation becomes \[\rho \frac{\partial\vec{u}}{\partial t} + \rho (\vec{u}\cdot \gradient) \vec{u} + \gradient P = (\lambda + 2\mu) \gradient(\gradient\cdot \vec{u}) - \mu \gradient \times \gradient \times \vec{u} \] Equation (\ref{blacksters3}) is the energy equation. \(C_v\) is the heat capacity at constant volume. \(\Phi^{\text{(visc)}}\) is the nonlinear viscous dissipation function, and \(\kappa\) is the thermal conduction coefficient. Equation (\ref{blacksters4}) is the ideal gas law. \(R\) is the gas constant, given by \(C_p-C_v\). Since \(\gamma = C_p/C_v\), the gas constant can also be written as \[R = (\gamma-1)C_v.\]

Chapter 3: Reflection and transmission for normal incidence

Derive the reflection and transmission pressure coefficients for normal incidence of plane waves on a boundary. Check the results by assessing the limits. [answer]

On one side of the boundary (impedance \(Z_1\)) there is a pressure of \(p_i + p_r\). On the other side of the boundary (impedance \(Z_2\)) there is a pressure \(p_t\). Begin by noting that there cannot be any force at the boundary. That is, \(p_i + p_r = p_t\), or dividing by \(p_i\), \begin{align}\label{lskfjls}\tag{i} 1 + R = T\,. \end{align} Also note that the particle velocity must be continuous at the boundary: \(u_i + u_r = u_t\). Using the plane wave impedance relation \(u= p/Z\), the above relation becomes \begin{align*} \frac{p_i}{Z_1} - \frac{p_r}{Z_1} &= \frac{p_t}{Z_2}\\ p_i - p_r &= \frac{Z_1}{Z_2} p_t \end{align*} Dividing the above equation by \(p_i\) gives \begin{align} 1 - R &= \frac{Z_1}{Z_2} T \label{lksjfdlj}\tag{ii} \end{align} Combining equations (\ref{lskfjls}) and (\ref{lksjfdlj}) yields \begin{align}\label{lksdfsff}\tag{iii} T = \frac{2}{1+Z_1/Z_2}\,. \end{align} Combining equation (\ref{lksdfsff}) with equation (\ref{lskfjls}) gives \begin{align}\label{lkref}\tag{iv} R = \frac{1- Z_1/Z_2}{1+Z_1/Z_2}\,. \end{align} Equations (\ref{lksdfsff}) and (\ref{lkref}) make sense because they match the following limits:
When \(Z_1/Z_2 \to 0\), the incident wave experiences a rigid boundary, and an in-phase reflection and pressure doubling at boundary is expected. Indeed, equation (\ref{lkref}) goes to \(1\) while equation (\ref{lksdfsff}) goes to \(2\).

When \(Z_1/Z_2 \to \infty\) the incident wave experiences a pressure-release boundary, and an out-of-phase reflection and zero transmission at boundary is expected. Indeed, equation (\ref{lkref}) goes to \(-1\) while equation (\ref{lksdfsff}) goes to \(0\).

Finally, when \(Z_1/Z_2 = 1\), the incident wave does not experience a boundary, and no reflection and perfect transmission is expected. Indeed, equation (\ref{lkref}) goes to \(0\) and equation (\ref{lksdfsff}) goes to \(1\).
Derive the power reflection and transmission coefficients. How does the result relate to the first law of thermodynamics. [answer]

Recall that the power is given by \(W = \oint \vec{I} \cdot d\vec{S}\), which for a plane wave simply reads \(p_\text{rms}^2 S/Z\). What is curious about this result is that the power in a plane wave is infinite, because the pressure extends over the infinite surface, and the integral of a constant over all space diverges. However, never mind this curiosity; it is resolved because the ratio of powers is taken, and thus the surface area cancels. The power reflection coefficient is \begin{align*} r = \frac{W_r}{W_i} = \frac{p_{r, \text{rms}}^2 S/Z_1}{p_{i, \text{rms}}^2 S/Z_1} \end{align*} Critically, note that the ratio of the rms pressures equals the ratio of the pressures, because the reflected wave has the same waveform as the incident wave in linear acoustics. The reflection coefficient is therefore simply \begin{align*} r = \frac{p_r^2}{p_i^2} = R^2\,. \end{align*} Meanwhile, the transmission coefficient is \begin{align*} \tau &= \frac{W_t}{W_i}\\ &= \frac{p_{t, \text{rms}}^2 S/Z_2}{p_{i, \text{rms}}^2 S/Z_1}\\ &= \frac{p_t^2/Z_2}{p_i^2/Z_1}\\ &= T^2 \frac{Z_1}{Z_2}\,. \end{align*} Evidently, since \begin{align*} R^2 &= \frac{1+(Z_1/Z_2)^2 - 2Z_1/Z_2}{1+(Z_1/Z_2)^2 + 2Z_1/Z_2}\\ T^2 &= \frac{4}{1 +(Z_1/Z_2)^2 + 2Z_1/Z_2} \end{align*} the conservation of power is recovered, i.e., \begin{align*} r + \tau &= R^2 + T^2 \frac{Z_1}{Z_2}\\ &= \frac{1+(Z_1/Z_2)^2 - 2Z_1/Z_2}{1+(Z_1/Z_2)^2 + 2Z_1/Z_2} + \frac{4 Z_1/Z_2}{1 +(Z_1/Z_2)^2 + 2Z_1/Z_2} \\ &= \frac{1+(Z_1/Z_2)^2 + 2Z_1/Z_2}{1+(Z_1/Z_2)^2 + 2Z_1/Z_2}\\ &= 1\,, \end{align*} and the result obeys the first law of thermodynamics.
Derive \(R\) and \(T\) due to change in cross-sectional surface area. [answer]

If there is a change in surface area in a medium, then \(1+R = T\) as before (force-free surface), but now the volume velocity \(q\) must be conserved at the junction, \begin{align*} q_i + q_r &= q_t\\ S_1 u_i + S_1 u_r &= S_2 u_t, \end{align*} where the definition of volume velocity has been used to obtain the second line above. Invoking the plane wave impedance relation gives \begin{align*} \frac{S_1}{Z} p_i - \frac{S_1}{Z} p_r &= \frac{S_2}{Z} p_t\\ p_i - p_r &= \frac{S_2}{S_1}p_t\\ 1- R&= \frac{S_2}{S_1}T \end{align*} Combining the above with \(1+R = T\) gives \begin{align*} T &= \frac{2S_1}{S_1+S_2} \,.\\ &= \frac{2}{1+S_2/S_1} \end{align*} and \begin{align*} R &= \frac{1 -S_2/S_1}{1+S_2/S_1}\,. \end{align*} Again a physical interpretation is provided:
For the case that the boundary is replaced by a rigid wall, \(S_2/S_1 \to 0\). Appropriately, \(R \to 1\) and \(T\to 2\).

For the case that the boundary is replaced by a pressure release surface, \(S_2/S_1 \to \infty\). Appropriately, \(R \to -1\) and \(T\to 0\).

Finally, for the degenerate case of no boundary, \(S_2/S_1 \to 1\). Appropriately, \(R \to 0\) and \(T\to 1\).
What is an implicit assumption about the expressions for \(R\) and \(T\) due to change in cross-sectional surface area? [answer]

An implicit assumption is that the wavelength is much longer than the characteristic length scale of the change in area. This is because the acoustic wave must maintain its plane-wave nature at the junctio for the the simple derivation above to hold. For example, if the change in surface area is due to sharp corners at the junction of two pipes of two different cross sectional areas, then the scattering off these corners must be neglected; the scattering is minimal for the case when the corners are of a dimension much smaller than a wavelength.
Derive \(R\) and \(T\) due to change in both surface area and impedance. [answer]

If there is a change in both surface area and impedance, then \(1+R = T\) and \begin{align*} q_i + q_r &= q_t\\ S_1 u_i + S_1 u_r &= S_2 u_t, \end{align*} where the definition of volume velocity has been used to obtain the second line above. Invoking the plane wave impedance relation gives \begin{align*} \frac{S_1}{Z_1} p_i - \frac{S_1}{Z_1} p_r &= \frac{S_2}{Z_2} p_t\\ p_i - p_r &= \frac{S_2 Z_1}{S_1 Z_2}p_t\\ 1- R&= \frac{S_2 Z_1}{S_1 Z_2}T \end{align*} Combining the above with \(1+R = T\) gives \begin{align*} T &= \frac{2S_1 Z_2}{S_1 Z_2 +S_2 Z_1} \,.\\ &= \frac{2}{1+Z_1S_2/Z_2S_1} \end{align*} and \begin{align*} R &= \frac{1 -Z_1S_2/Z_2S_1}{1+Z_1S_2/Z_2S_1}\,. \end{align*} The above results can easily be recast using the notion of acoustic impedance, which is defined as \(Z_\text{ac} = Z_\text{sp, ac}/S\): \begin{align*} T &= \frac{2}{1+Z_\text{ac,1}/Z_\text{ac,2}}\\ R &= \frac{1 -Z_\text{ac,1}/Z_\text{ac,2}}{1+Z_\text{ac,1}/Z_\text{ac,2}}\,. \end{align*}
Derive the power reflection and transmission coefficients for the general case in problem (5). [answer]

The setup is much the same as in problem (3), only this time accounting for the change in surface area as well as the change in impedance at the boundary: \begin{align*} r = \frac{p_r^2}{p_i^2} = R^2\,. \end{align*} Meanwhile, the transmission coefficient is \begin{align*} \tau &= \frac{W_t}{W_i}\\ &= \frac{p_{t, \text{rms}}^2 S_2/Z_2}{p_{i, \text{rms}}^2 S_1/Z_1}\\ &= \frac{p_t^2/Z_\text{ac,2}}{p_i^2/Z_\text{ac,1}}\\ &= T^2 \frac{Z_\text{ac,1}}{Z_\text{ac,2}}\,. \end{align*} You can check for yourself that power is conserved, but the algebra is identical to that of problem (3).
Calculate pressure in a semi-infinite shock tube with a rigid termination at \(x=0\) due to a finite step shock. The initial conditions are \begin{align*} p(x,0) &= A[H(x) - H(x-L)]\\ u(x,0) &= 0 \end{align*} and the boundary condition is \(u(0,t) =0\). [answer]

The general pressure solution is \begin{align*} p(x,t) = f(x-c_0t) + g(x+c_0t)\,. \end{align*} Using the plane wave impedance relation, the corresponding particle velocity is \begin{align*} u(x,t) = \frac{1}{\rho_0c_0}[f(x-c_0t) - g(x+c_0t)]\,. \end{align*} Matching the initial velocity condition gives \begin{align*} u(x,0) = \frac{1}{\rho_0c_0}[f(x) - g(x)] =0 \end{align*} which means that \(f(x) = g(x)\). Thus the pressure and particle velocity solution reads \begin{align*} p(x,t) &= f(x-c_0t) + f(x+c_0t)\\ u(x,t) &= \frac{1}{\rho_0c_0}[f(x-c_0t) - f(x+c_0t)]\,. \end{align*} Next, matching the initial pressure condition \(p(x,0) = A[H(x) - H(x-L)]\) gives \begin{align*} p(x,0) = f(x) = \frac{A}{2}[H(x) - H(x-L)]\,. \end{align*} The pressure and particle velocity solution then reads \begin{align*} p(x,t) &= \frac{A}{2}[H(x-c_0t) - H(x-L-c_0t) + H(x+c_0t) - H(x-L+c_0t)]\\ u(x,t) &= \frac{A}{2\rho_0c_0}[H(x-c_0t) - H(x-L-c_0t) - H(x+c_0t) + H(x-L+c_0t)]\,, \end{align*} or, in terms of the "rect'' function (see footnote on page 10 of Blackstock for the definition), \begin{align*} p(x,t)&= \frac{A}{2}\bigg[\text{rect }\bigg(\frac{x-c_0t}{2L}\bigg) + \text{rect }\bigg(\frac{x+c_0t}{2L}\bigg)\bigg]\\ u(x,t)&=\frac{A}{2\rho_0c_0}\bigg[\text{rect }\bigg(\frac{x-c_0t}{2L}\bigg) - \text{rect }\bigg(\frac{x+c_0t}{2L}\bigg)\bigg]\,. \end{align*} The solution for negative \(x\) is disregarded. Note that the above particle velocity solution satisfies the boundary condition \(u(0,t) =0\). I don't know Dr. Blackstock makes a fuss about satisfying the boundary condition on page 120 (''But this is not a sufficient definition of \(f\) to satisfy the last condition...'').
What is the volume velocity at the center of a spherically converging wave? [answer]

The volume velocity vanishes at the center of a spherical wave. A spherically converging wave is spherically symmetric, and therefore the particle velocities (which only have a radial component) coming from all directions towards the focus cancel each other out at the focus.
☸ Calculate pressure in bursting balloon due to a finite step shock set off by the initial conditions \begin{align} p(r,0) &= A[H(r)- H(r-r_0)]\label{initialcondos1}\tag{i}\\ u(r,0) &= 0\,.\label{initialcondos2}\tag{ii} \end{align} Note that the volume velocity \(q = Su\) must vanish at \(r =0\) (see previous problem for explanation): \begin{align}\label{zero vv}\tag{iii} \lim_{r\to 0} q = \lim_{r\to 0} Su = \lim_{r\to 0} 4\pi r^2 u = 0\,. \end{align} Outline: Use the velocity potential \(\phi\), recalling that \(p = -\rho_0 \phi_t\) and \(u = \phi_r\). Match the initial velocity condition and conclude that \(g(r) = -f(r)\). Apply this result \(p(r,t)\) and \(u(r,t)\), calculate \(q(r,t) = \pi r^2 u(r,t)\), and apply the limit above to show that \(f\) is even and \(f'\) is odd. Then apply the initial pressure condition to \(p(r,t)\), solve for \(f'(t)\), replace \(r\) with \(r\pm c_0 t\). Substitute the resulting \(f'(r\pm c_0 t)\) into \(p(r,t)\). [answer]

Since the sound obeys the spherically symmetric wave equation, the velocity potential is of the form \begin{align*} \phi &= \frac{f(r -c_0 t)}{r} + \frac{g(r +c_0 t)}{r}\,. \end{align*} The pressure is therefore \begin{align}\label{form of p}\tag{iv} p(r,t) &= -\rho_0 \phi_t = \rho_0 c_0\frac{f'(r -c_0 t) -g'(r +c_0 t)}{r}\,, \end{align} and the particle velocity is \begin{align}\label{form of u}\tag{v} u(r,t) &= \phi_r = -\frac{f(r -c_0 t) + g(r + c_0 t)}{r^2} + \frac{f'(r -c_0 t) + g'(r + c_0 t)}{r} \,. \end{align} Applying the initial condition given by equation (\ref{initialcondos2}) on equation (\ref{form of u}) gives \begin{align*} \frac{f(r) + g(r)}{r^2} = \frac{f'(r ) + g'(r)}{r} \end{align*} This equality is guaranteed if \(g(r) = -f(r)\), because this implies that \(g'(r) = -f'(r)\) (though the converse is not necessarily true). Therefore, equation (\ref{form of p}) becomes \begin{align}\label{form of p'}\tag{vi} p(r,t) &= \rho_0 c_0\frac{f'(r -c_0 t) + f'(r +c_0 t)}{r}\,, \end{align} and equation (\ref{form of u}) becomes \begin{align*} u(r,t) &= -\frac{f(r -c_0 t) - f(r + c_0 t)}{r^2} + \frac{f'(r -c_0 t) - f'(r + c_0 t)}{r} \,. \end{align*} The volume velocity is therefore \begin{align} q &= Su = 4\pi r^2 u \notag\\ &= -4\pi [f(r -c_0 t) - f(r + c_0 t)] + 4\pi r [f'(r -c_0 t) - f'(r + c_0 t)] \,.\label{q}\tag{vii} \end{align} The condition given by equation (\ref{zero vv}) is applied to equation (\ref{q}): \begin{align} \lim_{r\to 0}q &= -4\pi [f( -c_0 t) - f(c_0 t)] = 0\notag\\ \implies f(-c_0 t) &= f(c_0 t) \,.\label{limq}\tag{viii} \end{align} Taking the derivative of equation (\ref{limq}) gives \begin{align}\label{oddy}\tag{ix} -f'(-c_0 t) &= f'(c_0 t)\,, \end{align} i.e., that \(f'\) is odd.

Meanwhile, the initial condition given by equation (\ref{initialcondos1}) is applied to equation (\ref{form of p'}): \begin{align*} A[H(r) - H(r-r_0)] &= 2\rho_0 c_0\frac{f'(r)}{r} \end{align*} Solving the above for \(f'(r)\) gives \begin{align}\label{fprime}\tag{x} f'(r) &= \frac{rA[H(r) - H(r-r_0)]}{2\rho_0 c_0} \end{align} Enforcing equation (\ref{oddy}) (the oddness of \(f'\)) on equation (\ref{fprime}) requires that \(f'\) is defined for \(-r\) as well as \(+r\). This can be achieved using the rectangle function, where \(\text{rect }\big( \frac{x-x_0}{w}\big) = H(x-x_0 + w/2) - H(x-x_0 - w/2)\): \begin{align*} f'(r) = \frac{rA}{2\rho_0 c_0}\text{ rect } \bigg(\frac{r}{2r_0}\bigg) \end{align*} Therefore, \begin{align}\label{final f'}\tag{xi} f'(r\pm c_0t) = \frac{A}{2\rho_0 c_0}(r\pm c_0t)\text{ rect } \bigg(\frac{r\pm c_0 t}{2r_0}\bigg) \end{align} Substituting equation (\ref{final f'}) into equation (\ref{form of p'}) gives the solution: \begin{align*} p(r,t) = \frac{A}{2r} \bigg[(r-c_0t)\text{ rect }\Big(\frac{r-c_0t}{2r_0}\Big) + (r+c_0t)\text{ rect }\Big(\frac{r+c_0t}{2r_0}\Big)\bigg] \end{align*}
☸ Consider a sphere of radius \(r_0\). At \(r = r_0\), the incident pressure wave is given by \(p_\mathrm{in}(t)\). The pressure solution is therefore of the form \begin{align}\label{form of pressuriners}\tag{i} p = \frac{r_0}{r}p_\mathrm{in}(t + r/c_0) + \frac{F(t-r/c_0)}{r}, \end{align} where \(F(t-r/c_0)/r\) corresponds to the wave emerging through the focus. Determine \(F(t-r/c_0)\) in terms of \(p_\mathrm{in}\). What is the pressure at the center of a sphere? Outline: Given equation (\ref{form of pressuriners}), find \(u\), where \(\tilde{F}\) is the antiderivative of \(F\) and \(\tilde{p}\) is the antiderivative of \(p\). Take the limit as \(r\to 0\), for which the volume velocity \(4\pi r^2 u = 0\). Solve for \(\tilde{F}\) and obtain \(F(t) = -r_0 p_\text{in}(t)\). [answer]

First, apply the momentum equation for a spherical wave, \(\rho_0\dot u = -p_r\), to equation (\ref{form of pressuriners}): \begin{align*} \rho_0 \frac{\partial u}{\partial t} &= \frac{F'(t-r/c_0) - r_0p_\mathrm{in}'(t + r/c_0)}{c_0 r} + \frac{F(t-r/c_0)+ r_0 p_\mathrm{in} (t + r/c_0)}{r^2} \end{align*} Solving the above for \(u\) by integration over time gives \begin{align} u &= -\frac{1}{\rho_0}\int \frac{\partial p}{\partial t}\, dt\notag\\ &= \frac{F(t-r/c_0) - r_0p_\mathrm{in}(t + r/c_0)}{\rho_0c_0 r} + \frac{\tilde{F}(t-r/c_0)+ r_0 \tilde{p}_\mathrm{in} (t + r/c_0)}{\rho_0 r^2}\,,\label{refthis}\tag{ii} \end{align} where \(\tilde{p}\) is the antiderivative of \(p\), and \(\tilde{F}\) is the antiderivative of \(F\). When the boundary condition \(\lim_{r\to 0} q = \lim_{r\to 0} 4\pi r^2 u = 0\) is applied to equation (\ref{refthis}), the first term of equation (\ref{refthis}) vanishes, and the second term gives \begin{align*} \frac{4\pi}{\rho_0}[\tilde{F}(t) + r_0 \tilde{p}_\mathrm{in}(t)] &= 0\,. \end{align*} Solving the above for \(\tilde{F}(t)\) gives \begin{align*} \tilde{F}(t) = -r_0\tilde{p}_\mathrm{in}(t) \quad \implies \quad F(t) = -r_0 p_\mathrm{in}(t)\,. \end{align*} Substituting \(F(t) = -r_0 p_\mathrm{in}(t)\) into equation (\ref{form of pressuriners}) gives the solution \begin{equation}\label{pressuresolutioneerses} p = \frac{r_0}{r}p_\mathrm{in}(t + r/c_0) - \frac{r_0}{r}p_\mathrm{in}(t-r/c_0),\tag{iii} \end{equation} The first term corresponds to the incoming wave, and the second term corresponds to the outgoing wave. Note that the outgoing wave is out of phase with respect to the incoming wave.

What happens at \(r=0\) (the focus)? The limit of equation (\ref{pressuresolutioneerses}) is taken: \begin{align*} \lim_{r\to 0}p &= \lim_{r\to 0}\frac{r_0}{r}\bigg[p_\mathrm{in}(t + r/c_0) - p_\mathrm{in}(t-r/c_0)\bigg]\\ &=\lim_{r\to 0}\frac{r_0}{r}\bigg[p_\mathrm{in}(t) +\frac{r}{c_0}p'_\mathrm{in}(t)- p_\mathrm{in}(t)+ \frac{r}{c_0} p_\mathrm{in}'(t)\bigg]\\ &=\frac{2r_0}{c_0}p'_\mathrm{in}(t) \end{align*} In the second equality above, the function is Taylor expanded to first order, and the higher-order terms are dropped. The conclusion is that the pressure at the center of the sphere is proportional to the time derivative of the incident pressure. \begin{align*} p(r=0,t) = \frac{2r_0}{c_0}p'_\mathrm{in}(t) \end{align*}
Given the previous result, what happens to the phase at the focal point of a focused sound beam? [answer]

The phase undergoes a \(180^\circ\) inversion.
☸ Derive the reflection and transmission coefficients \(R\) amd \(T\) for the three-medium problem, where the three media are labelled I, II, and III, as described on p. 168 of Fundamentals of Physical Acoustics. Assume that \(P_{\mathrm{I}} = A_1 e^{-jk_1x} + B_1 e^{jk_1x}\), \(P_{\mathrm{II}} = A_2 e^{-jk_2x} + B_2 e^{jk_2x}\), and \(P_{\mathrm{III}} = A_3 e^{-jk_3(x-l)}\) and apply the boundary conditions at the two interfaces. [answer]

The problem is worked out here.

Chapter 4: Impedance tubes and \(k\ell \ll 1 \) impedances

This short video summarizes questions 1-3.

☸ How is the impedance \(Z_n\) of an unknown material measured in an impedance tube, where the impedance of the medium (e.g., air) is \(Z_0\)? [answer]

Start with the general solution \(P(x)\) and \(U(x)\) of the 1D Helmholtz equation for plane traveling waves. The general solution for pressure is \[P = Ae^{-jkx} + Be^{jkx},\] and division by \(Z_0\), the impedance of the medium, gives the particle velocity: \[U = \frac{A}{Z_0} e^{-jkx} - \frac{B}{Z_0}e^{jkx}\,.\] Define \(x=l-d\), where \(x=0\) corresponds to the location of the source, and \(d=0\) corresponds to the location of the load, i.e., \(d\) is a coordinate pointing in the opposite direction as \(x\) and offset by a distance \(l\). The pressure and particle velocity become \begin{align*} P &= Ae^{-jkl} e^{jkd} + Be^{jkl} e^{-jkd}\\ U &= \frac{A}{Z_0} e^{-jkl}e^{jkd} - \frac{B}{Z_0}e^{jkl}e^{-jkd} \end{align*} Call \(P_i \equiv A e^{-jkl}\) and \(P_r \equiv B e^{jkl}\). Then the above becomes \begin{align*} P &= P_i e^{jkd} + P_r e^{-jkd}\\ &= P_i e^{jkd} (1 + R\, e^{-2jkd})\,.\\ U&= \frac{P_i}{Z_0} e^{jkd} - \frac{P_r}{Z_0} e^{-jkd}\\ &= \frac{P_i}{Z_0}e^{jkd} (1 - Re^{-2jkd}) \end{align*} Note from the above that \(P(d=0) \,=\, P_i (1 + R)\), and that \(U(d=0) \,=\, \frac{P_i}{Z_0} (1 - R)\). Calculate \(P(d=0)/U(d=0)\) to find \(Z_n\), the impedance of the load, in terms of the reflection coefficient \(R\): \begin{align*} Z_n = Z_0 \frac{1+R}{1-R} \end{align*} If \(R\) (both magnitude and phase) can be found, then the complex impedance \(Z_n\) of the unknown load can be found.
How is the magnitude \(|R|\) of the reflection coefficient \(R\) found? [answer]

\(|R|\) is found by measuring the "standing wave ratio," or \(\text{SWR}\). The standing wave ratio is the ratio \(|P_\text{max}|/|P_\text{min}|\), where \(P_\text{max} = P_i(1+R)\) is the maximum pressure magnitude and where \(P_\text{min} = P_i(1-R)\) the minimum pressure magnitude. Therefore, \[\text{SWR} = \frac{1+|R|}{1-|R|}.\] This relation is inverted for \(|R|\): \[|R| = \frac{\text{SWR} - 1}{\text{SWR}+ 1}\,.\]
How is the phase \(\psi\) of \(R = |R|e^{j\psi}\) determined? [answer]

Take the magnitude of \(P=P_ie^{jkd}(1-R e^{-2jkd})\) by writing \(R = \rho e^{j\psi}\): \begin{align*} |P| &= P_i\sqrt{(1+ \rho e^{j(\psi - 2kd)})(1+ \rho e^{-j(\psi - 2kd)})} \\ &= P_i\sqrt{1 + \rho^2 + \rho [e^{-j({\psi - 2kd})} + e^{j(\psi - 2kd)}]}\\ &= P_i\sqrt{1 + \rho^2 + 2\rho \cos (\psi - 2kd) }\,. \end{align*} Apparently, \(|P|\) attains a maximum for \(\cos (\psi - 2kd) = 1\), or \[(kd)_\text{max} = \frac{\psi}{2},\] and a minimum for \(\cos (\psi - 2kd) = 0\), or \[(kd)_\text{min} = \frac{\psi}{2} \pm \frac{\pi}{2}\,. \] Thus the phase of reflection coefficient is found by finding the distance \(d\) to either the maximum or the minimum in the pressure field.
How is the attenuation coefficient \(\alpha\) measured? [answer]

By definition, \(\alpha\) is the ratio of absorbed to incident power. Note that by energy conservation, the incident power is the sum of reflected power and the absorbed power. Thus, \[\alpha = \frac{W_\text{absorbed}}{W_\text{incident}} = \frac{W_\text{incident}-W_\text{reflected}}{W_\text{incident}} = 1- \frac{W_\text{reflected}}{W_\text{incident}} = 1 - |R|^2\,.\]
What is the relationship between impedance, reactance, resistance, inductance, and capacitance? [answer]
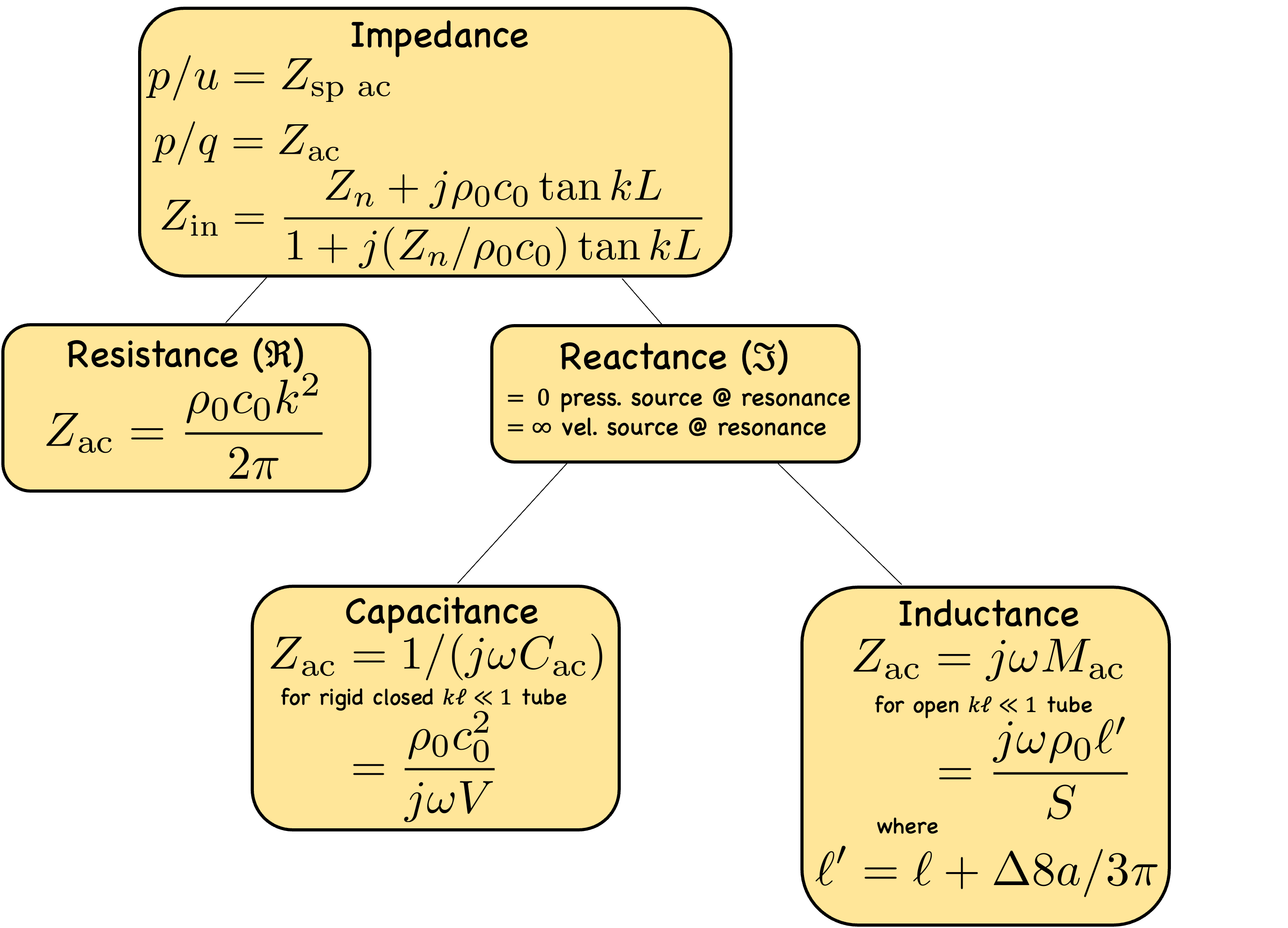
For a pressure source, the impedance at the resonance frequency goes to what quantity? [answer]

For a pressure source, the impedance goes to \(0\) for resonance. A small amount of effort causes a huge flow, and impedance is effort/flow.
For a velocity source, the impedance at the resonance frequency goes to what quantity? [answer]

For a velocity source, the impedance goes to \(\infty\) for resonance. A small amount of flow at the source results in a huge pressure field.
Derive \(Z_\text{ac}\) for mass-like and spring-like behaviours, appealing to Newton's law of motion and Hooke's constitutive relation. [answer]

Recall that the acoustic impedance is \(Z_\text{ac} = p/q\), where \(q = Su\) is the volume velocity. Therefore, for mass-like behaviour, \[Z_\text{ac} = \frac{p}{Su} = \frac{f/S}{Su} = \frac{M \dot{u}}{S^2 u} = \frac{j\omega M}{S^2} = j\omega M_\text{ac}\,.\] Meanwhile, for spring-like behaviour, \[Z_\text{ac} = \frac{p}{Su} = \frac{f/S}{S\dot{x}} = \frac{K x}{S^2 j\omega x} = \frac{K }{S^2 j\omega } = \frac{K_\text{ac} }{j\omega } =1/j\omega C_\text{ac}\,,\] where \(M_\text{ac}\) is the acoustic mass, \(K_\text{ac}\) is the acoustic stiffness, and \(C_\text{ac}\) is the acoustic compliance.
In question (1) of this section, \(Z_n\) was calculated by evaluating \(P/U\) at \(d=0\) (or \(x = L\) which corresponds to the location of the load). Now calculate the input impedance \(Z_\text{in}\), which is \(P/U\) at \(d=L\) (or \(x=0\)) in terms of \(Z_n\), the impedance of the load. Let \(P(x) = A \cos{kx} + B\sin{kx}\). [answer]

Using the momentum equation, the particle velocity is found: \[U(x) = -\frac{1}{j\omega \rho_0} \frac{dP}{dx} = \frac{A}{j\rho_0 c_0} \sin kx - \frac{B}{j\rho_0 c_0} \cos kx\,.\] Why must the momentum equation must be used here, while the impedance relation could be used in problem (1)? It's because these are standing waves (left-going and right-going components are already baked in), while those were traveling waves (which superpose to give standing waves). The impedance relation \(p/u = Z\) applies to what type of wave: standing or traveling?

The coefficients \(A\) and \(B\) are found by applying the boundary conditions. At \(x=L\), \begin{align*} Z_n = \frac{P(L)}{U(L)} &= j\rho_0 c_0 \frac{A\cos kL + B\sin kL}{A\sin kL - B\cos kL}\\ &= j\rho_0 c_0 \frac{A/B + \tan kL}{A/B \tan kL - 1}\\ \implies \frac{A}{B} &= j \frac{Z_n/\rho_0 c_0 + j\tan kL}{1 + j(Z_n/\rho_0 c_0) \tan kL}\,. \end{align*} Meanwhile, at \(x=0\), \begin{align*} Z_\text{in} = \frac{P(0)}{U(0)} &= -j\rho_0 c_0 \frac{A}{B}\\ \implies \frac{A}{B} &= j \frac{Z_\text{in}}{\rho_0c_0} \end{align*} Setting the above two equations for \(\frac{A}{B}\) equal and solving for \(\frac{Z_\text{in}}{\rho_0 c_0}\) gives the input impedance in dimensionless form: \[\frac{Z_\text{in}}{\rho_0 c_0} = \frac{Z_n/\rho_0 c_0 + j\tan kL}{1 + j(Z_n/\rho_0 c_0) \tan kL} \,. \]
In the previous problem it was found that the input impedance in terms of the impedance of the load is \begin{equation}\label{Input impedance}\tag{2} \frac{Z_\text{in}}{\rho_0 c_0} = \frac{Z_n/\rho_0 c_0 + j\tan kL}{1 + j(Z_n/\rho_0 c_0) \tan kL} \,. \end{equation} What are the three special cases that follow from equation (\ref{Input impedance})? [answer]
1. For \(Z_n = 0\) (i.e., pressure release), \[Z_\text{in} = j \rho_0 c_0 \tan kL\,. \]
2. For \(|Z_n| \to \infty\) (i.e., rigid) \[Z_\text{in} = -j \rho_0 c_0 \cot kL\,.\]
3. For \(Z_n = \rho_0 c_0\) (i.e., impedance matching), \[Z_\text{in} = 1\]
Use equation (\ref{Input impedance}) to derive \(Z_\text{in}\) for a short closed cavity. "Short" means \(kL \ll 1\) and "closed" means \(Z_n \to \infty\). Find the acoustic impedance also. [answer]

Note that \(\tan kL \simeq kL \) for small \(kL\) and equation (\ref{Input impedance}) becomes \(Z_\text{in} = -j\rho_0c_0\cot{kL}\) for \(Z_n \to \infty\). Then, \(Z_\text{in} = \frac{\rho_0c_0}{jkL}\), or \[Z_\text{in} = \frac{\rho_0 c_0^2}{j\omega L}\,.\] However, the quantity that should be memorized for acoustic circuit analysis is the acoustic impedance, \[Z_\text{ac} = Z_\text{sp ac}/S = \rho_0 c_0^2/{j\omega L S^2} = \rho_0 c_0^2/{j\omega V}\,.\] See question (5) for the impedances that should be memorized.
What is the end correction for a flanged tube? Qualitatively describe the origin of the end correction. What about the end correction for an unflanged tube? [answer]

For a flanged tube, the end correction is \(\Delta L = 8a/3\pi\). That is to say, the effective length of a flanged tube is \(L + \Delta L\), and the effective length of an orifice is \(2\Delta L\). This end correction originate from the fact that the impedance due to a circular piston contains resistive (real) and reactive (imaginary) parts, of which the reactance dominates. Therefore, when sound arrives at the open end of a tube, "it sees, not zero load, but rather a load consisting mainly of a short continuation of the tube, \(\Delta L = 8a/3\pi\)" (Blackstock, pg. 151-152).

The unflanged tube has an end correction of \(\Delta L = 0.6133a\). This is a 20th-century result (Schwinger).
Use equation (\ref{Input impedance}) to find the input impedance \(Z_\text{in}\) for short open cavity, where "short" means \(kL \ll 1\) and "open" means \(Z_n \to 0\). Also find the acoustic impedance. [answer]

Equation (\ref{Input impedance}) in these limits reads \[Z_\text{in} = j\rho_0 c_0 kL',\] where \(L' = L + \Delta L\) (the end correction). The version that should be memorized, though, is the acoustic impedance, which is \[Z_\text{ac} = j\rho_0 c_0 kL/S\,.\]
Calculate the acoustic impedance of a Helmholtz resonator. What is the resonance frequency for a pressure source? [answer]

The Helmholtz resonator consists of capacitave (from the chamber), inductive (from the mass in the neck), and resistive (from the opening) elements. The three corresponding impedances should be added in series since the components appear in series in the resonator (bad reasoning, I know): \begin{align*} Z_\text{ac} &= Z_\text{ac}^{\text{cap}} + Z_\text{ac}^{\text{ind}} + Z_\text{ac}^{\text{res}}\\ &= \frac{\rho_0c_0^2}{j\omega V} + \frac{j\omega \rho_0 L'}{S} + \frac{\rho_0 c_0 k^2}{2\pi}\,. \end{align*} For a pressure source, the resonance frequency is found by setting the impedance (neglecting resistance) to \(0\): \begin{align*} \frac{\rho_0c_0^2}{j\omega V} + \frac{j\omega \rho_0 L'}{S} &= 0\\ \omega_0 &= c_0 \sqrt{S/L'V}\,. \end{align*}

How would you find the resonance frequency for a velocity source, for which \(Z_\text{in} = \infty\)?
Provide a few definitions of the quality factor \(Q\). [answer]

One common definition is \[Q = \frac{\omega}{\Delta \omega}\] where \(\Delta \omega\) is the bandwidth.

Another definition is \[Q = \frac{P_\text{max}}{P_\text{min}}\,,\] which is subtly different from the definition of \(\text{SWR}\). (But how? I actually don't know. Is it that Q is a complex quantity here, while the SWR is real?)

Yet another definition (Dr. Wilson's favourite), is \[Q = \text{ # of oscillations required to return to steady state }\]
Write the impedance of a bubble using the low-\(ka\) approximation of the spherical wave impedance and find the resonance frequency in terms of the ratio of specific heats, \(\gamma\). Note from the definition of adiabatic sound speed that \(\rho_0 c_0^2 = \gamma p_0\). [answer]

The spherical wave impedance is \begin{align*} Z &= \frac{\rho_0 c_0 }{1 + 1/jka}\\ &\to jka\rho_0c_0, \quad ka \ll 1\,. \end{align*} This is a specific acoustic impedance. To obtain an acoustic impedance, divide by \(S = 4\pi a^2\): \begin{align}\label{bubbblers}\tag{i} Z_\text{ac}^\text{ind} = \frac{j\omega a\rho_0}{4 \pi a^2} = \frac{j\omega \rho_0}{4\pi a} \end{align} Noting that this in the form of a mass-like impedance, a compliance-like impedance is sought to set up a resonance phenomenon: \begin{align} Z_\text{ac}^\text{cap} &= \frac{\rho_0 c_0^2}{j\omega V} = \frac{3\rho_0 c_0^2}{4j\omega \pi a^3}\,.\label{bubbbblers}\tag{ii} \end{align} The resonance frequency is found by combining equations (\ref{bubbblers}) and (\ref{bubbbblers}) and setting the total impedance equal to \(0\). At this juncture, also note that \(\rho_0c_0^2 = \gamma p_0\), since an expression involving this quantity is requested in the problem: \begin{align*} Z_\text{ac}^\text{tot} = \frac{3\gamma p_0}{4j\omega \pi a^3} + \frac{j\omega \rho_0}{4\pi a} = 0 \end{align*} Solving for \(\omega\) gives \begin{align*} \omega &= \frac{1}{a} \sqrt{\frac{3\gamma p_0}{\rho_0}}\\ f&= \frac{1}{2\pi a} \sqrt{\frac{3\gamma p_0}{\rho_0}}\,. \end{align*} This is a decent approximation because \(ka = 0.014\) for an air-water bubble.
What is the acoustic impedance of an orifice (a hole in a plate)? [answer]

The orifice has a resistive part due to the opening on both ends, as well as an inductive part: \begin{align*} Z_{\text{ac}} = \frac{2\rho_0c_0k^2}{2\pi} + \frac{j\omega\rho_0 L'}{S}\,, \end{align*} where the effective length of the orifice is \(L' = 2\Delta L\) (because the orifice has no length of its own), where \(\Delta L = 8a/3\pi\).
Derive the \(R\), \(T_2\), and \(T_3\) for a side branch, where each pipe has a different cross-sectional area and contains a different medium. Let the incident wave originate from a region with cross-sectional area \(S_1\), and let where the two branches have cross-sectional area of \(S_2\) and \(S_3\) respectively. [answer]

Chris has an nice way of doing this using circuit analysis. Here is how to find the reflection and transmission coefficients using the force-free boundary condition and continuity of volume velocity:

At the junction, there are two conditions, as in the case with a single change of cross-sectional surface area. The first condition is that there is no force at the junction, and the second condition is that volume velocity at the junction is continuous: \begin{align*} p_i + p_r = p_{t2} = p_{t3}\\ q_i + q_r = q_{t2} + q_{t3} \end{align*} Divide the first equation by \(p_i\) and call \(p_{t2}/p_i = p_{t3}/p_i \equiv T\): \begin{align*} 1 + R = T\,. \end{align*} Meanwhile, the second equation is written as \[S_1 u_i + S_1u_r = S_2 u_{t2} + S_3 u_{t3}\] Noting that \(Z = p/u\), gives \begin{align*} S_1 \frac{p_i}{Z_1} - S_1\frac{p_r}{Z_1} = S_2 \frac{p_{t2}}{Z_2} + S_3 \frac{p_{t3}}{Z_3}\,. \end{align*} Dividing by \(p_i\) results in \begin{align*} \frac{S_1}{Z_1}(1 - R) = T \frac{S_2}{Z_2} + T \frac{S_3}{Z_3}\,. \end{align*} The above quantities are written in terms of their acoustic impedances. \begin{align*} 1 - R &= Z_\text{ac,1} T ( Z_\text{ac,2}^{-1} + Z_\text{ac,3}^{-1}) \end{align*} The above equation is added to \(1+R = T\): \begin{align*} 2 & = Z_\text{ac,1} T ( Z_\text{ac,2}^{-1} + Z_\text{ac,3}^{-1}) + T\\ 2&= T [1 + Z_\text{ac,1} ( Z_\text{ac,2}^{-1} + Z_\text{ac,3}^{-1})] \end{align*} Solving for \(T\) gives \begin{align*} T &= \frac{2Z_\text{ac,1}^{-1}}{Z_\text{ac,1}^{-1} + Z_\text{ac,2}^{-1} + Z_\text{ac,3}^{-1}} \end{align*} Thus the reflection coefficient is \begin{align*} R &= T -1 = \frac{2Z_\text{ac,1}^{-1}}{Z_\text{ac,1}^{-1} + Z_\text{ac,2}^{-1} + Z_\text{ac,3}^{-1}} - 1\\ &=\frac{Z_\text{ac,1}^{-1} - Z_\text{ac,2}^{-1} - Z_\text{ac,3}^{-1}}{Z_\text{ac,1}^{-1} + Z_\text{ac,2}^{-1} + Z_\text{ac,3}^{-1}}\,. \end{align*}
How can a Helmholtz resonator be used as a filter? [answer]

Let a Helmholtz resonator be attached a side branch to a pipe, and let the medium be uniform. Thus \(Z_\text{ac,1} = Z_\text{ac,3}\) the reflection coefficient is \begin{align*} R &=-\frac{Z_\text{ac,2}^{-1}}{2Z_\text{ac,1}^{-1} + Z_\text{ac,2}^{-1}}\\ &= -\frac{Z_\text{ac,2}^{-1} Z_\text{ac,2}} {2Z_\text{ac,1}^{-1}Z_\text{ac,2} + Z_\text{ac,2}^{-1} Z_\text{ac,2}}\\ &= -\frac{1}{2Z_\text{ac,1}^{-1}Z_\text{ac,2} + 1} \end{align*} The impedance of the Helmholtz resonator goes to \(0\) at resonance. Thus the reflection coefficient becomes \(R = -1\). Therefore, at the resonance frequency of the Helmholtz resonator, all of the sound is sent back down the pipe from which it originated.
The reflection and transmission coefficients for the three-medium problem are \begin{align} R &= \frac{(1-Z_1/Z_3)\cos k_2\ell + j(Z_2/Z_3-Z_1/Z_2)\sin k_2\ell}{(1+Z_1/Z_3)\cos k_2\ell + j(Z_2/Z_3+Z_1/Z_2)\sin k_2\ell}\label{3R} \tag{3}\\ T &= \frac{2}{(1+Z_1/Z_3)\cos k_2\ell + j(Z_2/Z_3+Z_1/Z_2)\sin k_2\ell}\label{3T} \tag{4} \end{align} Find \(R\) and \(T\) for the special cases of \(k_2 \ell = n\pi\) and \(k_2 \ell = (2n-1)\pi/2\). [answer]

For \(k_2 \ell = n\pi\), equations (\ref{3R}) and (\ref{3T}) become \begin{align*} R &= \frac{(1-Z_1/Z_3)}{(1+Z_1/Z_3)}\\ T &= (-1)^n\frac{2}{(1+Z_1/Z_3)}\,. \end{align*} For \(k_2 \ell = (2n-1)\pi/2\): \begin{align*} R &= \frac{Z_2/Z_3-Z_1/Z_2}{Z_2/Z_3+Z_1/Z_2}\\ T &= j(-1)^n\frac{2}{Z_2/Z_3+Z_1/Z_2}\,. \end{align*}
How do equations (\ref{3R}) and (\ref{3T}) change for a homogeneous medium of three different cross-sectional areas \(S_1\), \(S_2\), and \(S_3\)? [answer]

The reflection and transmission coefficients become \begin{align*} R &= \frac{(1-S_3/S_1)\cos k\ell + j(S_3/S_2-S_2/S_1)\sin k\ell}{(1+S_3/S_1)\cos k\ell + j(S_3/S_2+S_2/S_1)\sin k\ell}\\ T &= \frac{2}{(1+S_3/S_1)\cos k\ell + j(S_3/S_2+S_2/S_1)\sin k\ell} \end{align*}
Use equation (\ref{3T}) to find \(T\) and \(\text{TL}\) for the case that \(k_2 \ell \ll 1\) and \(Z_2 \gg Z_1 = Z_3\). What might these conditions represent physically? [answer]
For \(k_2 \ell \ll 1\), equation (\ref{3T}) becomes \begin{align*} T &= \frac{2}{(1+1) + j(Z_2/Z_1)k_2\ell}\\ &=\frac{2}{2 + jk_2\ell\rho_2c_2/\rho_0c_0}\\ &=\frac{2}{2 + j\omega\ell\rho_2/\rho_0c_0}\\ &=\frac{1}{1 + j\omega m/2\rho_0c_0} \end{align*} where \(\ell\rho_2\) has been identified as the mass of medium \(2\). The transmission loss is therefore \[\text{TL} = -10 \log_{10}\tau = 10 \log_{10} \bigg\lbrack 1 + \bigg(\frac{\omega m}{2\rho_0 c_0} \bigg)^2\bigg\rbrack \] These conditions represent a thin wall or barrier of \(m = \text{mass}/\text{unit area}\) in air.
Take the high-frequency limit of the \(\text{TL}\) obtained in the previous quesiton. How many \(\text{SPL dB}/\text{octave}\) does this correspond to? What is this "law" referred to as? Which frequencies therefore tend to pass through a wall? How much more massive must the wall be to make the sound passing through a wall half as loud? [answer]
For \(\omega m/2\rho_0c_0 \gg 1\), equation the transmission loss becomes \begin{align*} \text{TL} &\simeq 10 \log_{10} \bigg\lbrack \bigg(\frac{\omega m}{2\rho_0 c_0} \bigg)^2\bigg\rbrack\\ &= 10 \log_{10} \bigg(\frac{\pi f m}{\rho_0 c_0} \bigg)^2\\ &= 20 \log_{10} \frac{\pi f m}{\rho_0 c_0} \end{align*} Thus the transmission loss is \(20\log_{10} 2 = 6 \text{ dB}/\text{octave}\). This is the so-called mass law for normal incidence. So the bass frequencies are heard through the wall. The criterion "half as loud" roughly corresponds to \(12 \text{ dB} \simeq 20 \log_{10} 4\), which would require the wall to be four times as massive.

Chapter 5: \(R\)-\(T\) for oblique incidence

This short video summarizes questions 1-9.

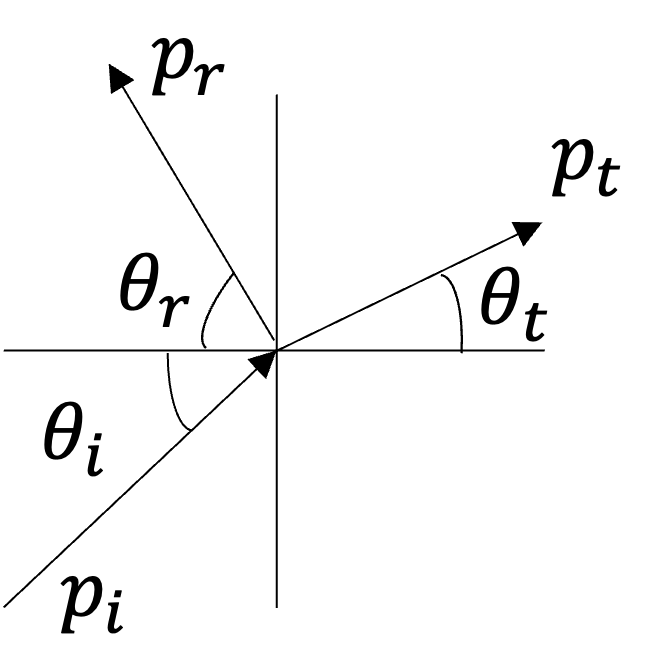
Consider wave propagation at the interface of two media, where the medium on the left is denoted "1" and has impedance \(Z_1\), and the medium on the right is denoted "2" and has impedance \(Z_2\), as shown below. The the horizontal direction is the rectangular \(x\)-coordinate and the vertical direction is the rectangular \(y\)-coordinate. \begin{align} p_i &= A_i \exp{(-jk_1x\cos\theta_i - jk_1y\sin\theta_i)}\label{pi} \tag{5}\\ p_r &= A_r \exp{(jk_1x\cos\theta_r - jk_1y\sin\theta_r)}\label{pr} \tag{6}\\ p_t &= A_t \exp{(-jk_2x\cos\theta_t - jk_2y\sin\theta_t)}\label{pt} \tag{7}\\ \end{align} What is the condition on the pressure at the boundary? Use this condition to derive the law of reflection and Snell's law. [answer]

At \(x=0\), there is no force on the boundary; thus \(p_i(x=0) + p_r(x=0) = p_t(x=0)\\\), or \begin{align*} A_i \exp{(- jk_1y\sin\theta_i)}+ A_r \exp{(- jk_1y\sin\theta_r)}&=A_t \exp{(- jk_2y\sin\theta_t)} \end{align*} For the above equation to hold, the phases must match, i.e., \(A_i + A_r = A_t\) or \(1 + R = T\): \[ k_1\sin\theta_i = k_1\sin\theta_r = k_2\sin\theta_t\] The first equality reveals the law of reflection, \[\theta_i = \theta_r\,,\] and the second equality reveals Snell's law, \[\frac{\sin\theta_i}{c_1} = \frac{\sin\theta_t}{c_2}\,.\]
There is another condition at the interface. What is it? Use it to derive the reflection and transmission coefficients \(R\) and \(T\). [answer]

The other condition is that the normal part of the particle velocity, namely the \(x\)-component of \(u\), is continuous across the boundary. Using equations (\ref{pi})-(\ref{pt}) in conjunction with the momentum equation \(-\frac{1}{j\omega \rho_0}\frac{\partial p}{\partial x}\) and the results of the previous question yields \begin{align*} \frac{1}{\omega \rho_1}\frac{\partial }{\partial x}(A_i e^{-jk_1x\cos\theta_i}) + \frac{1}{\omega \rho_1}\frac{\partial }{\partial x}(A_r e^{jk_1x\cos\theta_r}) = \frac{1}{\omega \rho_2}\frac{\partial }{\partial x}(A_t e^{-jk_2x\cos\theta_t}) \end{align*} Taking the derivatives above and matching the phases gives \begin{align*} \frac{-k_1}{\rho_1\omega}A_i\cos\theta_i + \frac{k_1}{\rho_1\omega}A_r\cos\theta_r &= -\frac{k_2}{\rho_2 \omega}A_t \cos\theta_t\\ \frac{-1}{\rho_1c_1}A_i\cos\theta_i + \frac{1}{\rho_1c_1}A_r\cos\theta_r &= -\frac{1}{\rho_2 c_2}A_t \cos\theta_t\\ \end{align*} Noting the law of reflection (\(\theta_i = \theta_r\)), multiplying through by \(-1\), and dividing by \(A_i\) results in \begin{align} 1-R = \frac{Z_1}{Z_2}\frac{\cos\theta_t}{\cos\theta_i}T\tag{i}\label{secondone} \end{align} Combining equation (\ref{secondone}) with \(1+R= T\) results in \begin{align*} R &= \frac{Z_2\cos\theta_i - Z_1\cos\theta_t}{Z_2\cos\theta_i + Z_1\cos\theta_t}\\ T &= \frac{2Z_2\cos\theta_i}{Z_2\cos\theta_i + Z_1\cos\theta_t} \end{align*}
Derive the power reflection and transmission coefficients \(r\) and \(\tau\). What is the cheap way of deriving \(\tau\)? [answer]

The power reflection coefficient is \begin{align*} r = \frac{W_r}{W_i} = \frac{S_rI_r}{S_iI_i}= \frac{I_r}{I_i} = \frac{|A_i|^2}{|A_r|^2} = |R|^2 \end{align*} where \(S_i\) is the cross-sectional area of the incident ray, and \(S_r\) is the cross-sectional area of the reflected ray. The areas of the same by the law of reflection.

Meanwhile, the cheap way to get \(\tau\) is to invoke the conservation of energy: \(\tau = 1-r\). The rigorous way accounts for the fact that the cross sectional area of the transmitted beam \(S_t\) is not the same as \(S_i\) due to Snell's law. In this approach, it is noted that \(S_t/S_i = \cos\theta_t/\cos\theta_i\) (see Blackstock's figure 5.5 on page 192), giving \begin{align*} \tau = \frac{W_t}{W_i} = \frac{S_tI_t}{S_iI_i}= \frac{S_t|A_t|^2/Z_2}{S_i|A_i|^2/Z_1} = \frac{Z_1\cos\theta_t}{Z_2\cos\theta_i}|T|^2\,. \end{align*}
What is the fancy name for the angle at which sound transmits perfectly from one medium to the next? Derive an expression for this angle. [answer]

It is called the angle of intromission. See here for the derivation, which was not rigorously derived in class, nor in Blackstock's text. Its derivation is straightforward, and I have shown the steps that lead to Blackstock's Eq. (B-14) in Sec. 5.B.2.a of Fundamentals of Physical Acoustics. Set \(T=1\), which corresponds to perfect transmission. Solve for \(\cos\theta_t\) and square the result. Meanwhile, solve Snell's law for \(\sin\theta_t\) and square it. Add these two equations and solve for \(\sin^2\theta_i\).
What is the condition for total internal reflection? What is name of the minimum angle \(\theta_i\) at which total internal reflection occurs? Find that angle. [answer]

The condition for total internal reflection is that the transmitted angle is \(\theta_t = 90^\circ\), and the angle \(\theta_i\) at which this occurs is called the critical angle, \(\theta_\text{crit}\). \(\theta_\text{crit}\) is given by Snell's law: \[\theta_\text{crit} = \arcsin \frac{c_1}{c_2}\]
Based on the figure below, which is larger: \(c_1\) or \(c_2\)? And from which direction of wave propagation does there exist a critical angle: \(c_1\) to \(c_2\), or \(c_2\) to \(c_1\)? [answer]

Sound (and light) traveling from a medium of higher wave speed into lower wave speed bend toward the normal. Thus \(c_1 > c_2\). There can exist a critical angle for wave propagation from \(c_2\) to \(c_1\).
In optics, a converging lens generally has a convex shape \(()\), while a diverging lens generally has a concave shape \()(\). But in acoustics, a converging lens generally has a concave shape \()(\), while a diverging lens generally has a convex shape \(()\). Why is this? [answer]

This is because in optics, light travels faster in air than in the material of the lens (e.g., a glass lens in air), while in acoustics, sound travels slower in air than the material of the lens (e.g., a water lens in air). For example, a converging lens bends light towards the local normal in the lens, so a convex shape is used in optics, while a concave shape is used in acoustics:
For \(\theta_i >\theta_\text{crit}\), what happens to equation (\ref{pt})? What is the term for the transmitted waves in the \(x\)-direction? [answer]

For \(\theta_i >\theta_\text{crit}\), \(\cos\theta_t\) is negative, because for \(\pi/2 < \psi <3\pi/2\), \(-1<\cos \psi <0\). Therefore, equation (\ref{pt}) becomes \begin{align*} p_t &= A_t \exp(\mp jk_2x \sqrt{1-\sin^2\theta_t}-jk_2y\sin\theta_t)\\ &= A_t \exp\bigg(\mp jk_2x \sqrt{1-(c_1/c_2)^2\sin^2\theta_i}-jk_2y\sin\theta_t\bigg)\\ &= A_t \exp\bigg(\pm k_2x \sqrt{(c_1/c_2)^2\sin^2(\theta_i) - 1}-jk_2y\sin\theta_t\bigg)\\ &= A_t \exp\bigg(- k_2x \sqrt{(c_1/c_2)^2\sin^2(\theta_i) - 1}-jk_2y\sin\theta_t\bigg)\,. \end{align*} Thus \(p_t\) decays exponentially in the \(x\) direction. Note that in the last line above, the \(-\) sign in the exponential is chosen because it is physical, i.e., exponential growth is not physical. These are called evanescent waves. The attenuation coefficient as identified as \[\alpha = k_2 \sqrt{(c_2/c_1)^2\sin^2\theta_i - 1}.\] For convenience, Dr. Blackstock also denotes the dimensionless quantity \(\sqrt{(c_2/c_1)^2\sin^2\theta_i - 1}\equiv b\).
☸ For \(\theta_i >\theta_\text{crit}\), what happens to the reflection coefficient \[R = \frac{Z_2\cos\theta_i - Z_1\cos\theta_t}{Z_2\cos\theta_i + Z_1\cos\theta_t}?\] Use the force-free boundary condition on the interface \(1+R=T\) to also determine what happens to the transmission coefficient for \(\theta_i >\theta_\text{crit}\). Find \(|T|\) as well. Use Dr. Blackstock's notation \(b\equiv\sqrt{(c_2/c_1)^2\sin^2\theta_i - 1}\). [answer]

As seen in the previous part, the quantity \(\cos\theta_t\) can be written as \(-j\sqrt{(c_2/c_1)^2\sin^2\theta_i - 1} = -jb\). Therefore, the reflection coefficient becomes \begin{align*} R &= \frac{Z_2\cos\theta_i + jb Z_1}{Z_2\cos\theta_i - jb Z_1}\\ &= \frac{\sqrt{Z_2^2\cos^2\theta_i + b^2Z_1^2}e^{j\arctan{bZ_1/Z_2\cos\theta_i}}}{\sqrt{Z_2^2\cos^2\theta_i + b^2Z_1^2}e^{-j\arctan{bZ_1/Z_2\cos\theta_i}}}\\ &= \exp\bigg[{2j\arctan\bigg({\frac{b}{\cos\theta_i}\frac{Z_1}{Z_2}}\bigg)}\bigg]\\ &= \exp(2j\psi) \end{align*} where \(\psi = \arctan\big({\frac{b}{\cos\theta_i}\frac{Z_1}{Z_2}}\big)\). The transmission coefficient \(T\) is therefore \[T = 1+\exp(2j\psi)\,,\] and \[|T| = \sqrt{2+2\cos2\psi}\,. \]
The mass law for oblique incidence was covered in class by considering the wall in two different ways. Qualitatively describe the boundary conditions at the wall and how one would obtain the reflection and transmission coefficients in both cases. [answer]

The first way was by considering the wall to be mass-like (i.e., only compliance, no stiffness). In that case, the pressure at the boundary is given by Newton's second law, i.e., \(p_i + p_r -p_t = m\partial u_x/\partial t\), where \(u_x\) is the normal component of the velocity. The other boundary condition is that the normal component of the velocities must match on either side of the boundary, i.e., \(u_i\cos\theta + u_r\cos\theta = u_t\cos\theta\) which gives \(1-R=T\) upon division by \(u_i\cos(\theta)\times\) the impedance of the propagation medium. These relations can be combined to get \(T\), \[T = \frac{1}{1+j\omega m \cos(\theta)/2\rho_0 c_0}\,,\] which recovers the special case of the three-medium problem considered in chapter 4. What is remarkable about \(T\) is that it equals \(1\) for \(\theta= 90^\circ\).

The second way is more refined, in which the wall's stiffness is incorporated. See here for the derivation. In short, the compliance of the wall makes the right-hand side of Newton's second law differ from the rigid case, but the normal component of the particle velocity condition is identical to that in the rigid case. The result is \[T = \frac{1}{1+(j\omega m \cos(\theta)/2\rho_0 c_0)[1-(f/f_0)^2\sin^4\theta]}\,.\] For a given angle, the coincidence frequency is the frequency at which \(T = 1\). Physically, coincidence is the matching of the trace speed to the natural flexural wave speed of the panel. Coincidence takes a massive hit to the transmission loss of a panel.
How does one calculate the power transmission coefficient \(\bar{\tau}\) for a composite wall, i.e., a wall with windows, doors, etc. How does one then calculate the composite transmission loss \(\text{TL}_\text{comp}\). [answer]

For composite walls, the power transmission coefficients are averaged by the area they occupy: \[\bar{\tau} = \frac{\sum_n S_n\tau_n}{\sum_n S_n}.\] Note that \(S\) can be in any unit of area. The composite transmission loss is \[\text{TL}_\text{comp} = -10 \log_{10}\bar{\tau}\,.\]

Chapter 6: Normal modes in Cartesian coordinates

Solve \(\xi_{xx}- \frac{1}{c^2}\xi_{tt} = 0\) for a fixed-fixed string for an arbitrary initial displacement \(\xi(x,0)\). How does the answer change for an initial velocity condition \(\dot{\xi}(x,0)\)? [answer]

Separation of variables and application of the fixed-fixed boundary condition leads to \begin{align}\tag{i}\label{xiexpanders} \xi(x,t) = \sum_{n=1}^{\infty} \sin(n\pi x/L)(a_n \cos\omega t + b_n\sin \omega t) \end{align} To find the expansion coefficients for the initial condition \(\xi(x,0)\), first note that \(b_n = 0\) in equation (\ref{xiexpanders}): \begin{align*} \xi(x,0) &= \sum_{n=1}^{\infty} a_n\sin(n\pi x/L) \end{align*} Invoking the orthogonality of sines gives \begin{align*} \int_0^L \xi(x,0)\sin(m\pi x/L) dx &= \sum_{n=1}^{\infty} a_n \int_0^L \sin(n\pi x/L)\sin(m\pi x/L)dx \\ \int_0^L \xi(x,0)\sin(m\pi x/L) dx &= \frac{L}{2}\sum_{n=1}^{\infty} a_n \delta_{nm}\\ \implies a_n &= \frac{2}{L}\int_0^L \xi(x,0) \sin(n\pi x/L) dx \end{align*} Thus the solution is \(\xi(x,t) = \sum_{n=1}^{\infty} a_n\sin(n\pi x/L)\), where \(a_n\) is given above.

To find the expansion coefficients for the initial condition \(\dot{\xi}(x,0)\), first note that the time derivative of equation (\ref{xiexpanders}) must be taken, \[\dot{\xi}(x,t) = \sum_{n=1}^{\infty} \sin(n\pi x/L)(-a_n \omega\sin\omega t + \omega b_n\cos \omega t)\,,\] from which evaluation at \(t=0\) shows that \(a_n = 0\): \[\dot{\xi}(x,0) = \omega \sum_{n=1}^{\infty} b_n\sin(n\pi x/L)\,.\] Invoking the orthogonality of sines gives \begin{align*} \int_0^L \dot{\xi}(x,0)\sin(m\pi x/L) dx &= \omega \sum_{n=1}^{\infty} b_n \int_0^L \sin(n\pi x/L)\sin(m\pi x/L)dx \\ \int_0^L \dot{\xi}(x,0)\sin(m\pi x/L) dx &= \frac{L\omega}{2}\sum_{n=1}^{\infty} b_n \delta_{nm}\\ \implies b_n &= \frac{2}{L\omega}\int_0^L \dot{\xi}(x,0) \sin(n\pi x/L) dx \end{align*} Thus the solution is \(\xi(x,t) = \sum_{n=1}^{\infty} b_n\sin(n\pi x/L)\), where \(b_n\) is given above.
☸ Without performing a calculation, which eigenmode(s) of a 1D string will contribute to the solution if the initial velocity condition is \(-u_0\) for \(0< x \leq L/2\) and \(u_0\) for \(L/2< x< L\)? [answer]

First of all, the \(n = 1, 3, 5\dots\) modes will not contribute because they violate the symmetry of the initial condition: these modes are even about \(L/2\), while the initial condition is odd about \(L/2\). Of the remaining \(n = 2, 4, 6\dots\) modes, only \(n=2,6,10\dots\) contribute. While the \(n=4,8,12\dots\) modes are odd about \(L/2\), their derivative is positive at \(x=L/2\), while the derivative of the initial condition is \(-\infty\) at \(x=L/2 \). This can be seen in the plots of the normalized standing waves vs. \(x/L\) below, where the red curve is the \(n = 4\) mode.
Given the expression for \(b_n\) from the first problem, calculate the expansion coefficients for a string that has an initial velicty of \(-u_0\) for \(0< x \leq L/2\) and \(u_0\) for \( L/2< x < L \) and thereby verify the result above. [answer]

The equation for \(b_n\) is \[b_n = \frac{2}{L\omega_n} \int_{0}^{L} \dot{\xi}(x,0)\sin \frac{n\pi x}{L}dx\] so for the initial velocity condition one obtains \begin{align*} b_n &= -\frac{2}{L\omega_n} \int_{0}^{L/2} \sin \frac{n\pi x}{L}dx + \frac{2}{L\omega_n} \int_{L/2}^{L} \sin \frac{n\pi x}{L}dx\\ &=\frac{2Lu_0}{(n\pi)^2 c}\big(2\cos\frac{n\pi}{2} -\cos n\pi - 1\big)\\ &=\begin{cases} 0\quad & n =\text{ odd}\\ 0\quad & n =4,8,12\dots\\ -4\quad& n = 2,6,10,14\dots \end{cases} \end{align*}
☸ What is the boundary condition at a free end of a string? Provide some rationale. Of which boundary condition of acoustics is the free-end boundary condition of a string reminiscent? And of which boundary condition in acoustics is the fixed-end boundary condition of a string reminiscent? [answer]

The boundary condition at a free end of a string is \(\partial \xi/\partial x = 0\). The reason is that the restoring force on the string is \(f= -\mathcal{T}\sin\theta \simeq -\mathcal{T}\theta\). At the free end of the string, \(x=\ell\), there is no element at \(\ell + \Delta x\) to pull the string up or down. Thus \(\theta = 0 \simeq\tan{\theta}\simeq\partial \xi/\partial x\). This condition is reminiscent of a rigid surface in acoustics because the derivative of the wave variable vanishes at that location.

The fixed-end boundary condition is \(\xi = 0\), which is reminiscent of a pressure-release boundary in acoustics.
☸ Solve \(\partial^2 p/\partial x^2 + k^2 p = 0\) for the boundary conditions \(dp/dx = 0\) and \(j\omega \rho_0 p + Z_n dp/dx = 0\) where \(Z_n = j\omega m\) for \(x=L\). \(dp/dx = 0\) is a rigid boundary condition, but what is \(j\omega \rho_0 p + Z_n dp/dx = 0\) called? Would this tube with a mass at one end sound good? [answer]

The general solution to the Helmholtz equation is \begin{align*} p = \sum_n (a_n\cos kx + b_n \sin kx)\,, \end{align*} the gradient of which is \begin{align*} \frac{dp}{dx} = \sum_n k(-a_n\sin kx + b_n \cos kx)\,. \end{align*} Since \(\frac{dp}{dx}\rvert_{x=0}= 0\), \(b_n = 0\), leaving \begin{align}\tag{i}\label{impyp} p = \sum_n a_n\cos kx \,. \end{align} Substituting equation (\ref{impyp}) into the boundary condition at \(x=L\), \(\rho_0 p +m\frac{dp}{dx} = 0\), gives \begin{align} \rho_0 p\big\rvert_{x=L} +m\frac{dp}{dx}\bigg\rvert_{x=L} &= 0\notag\\ \rho_0 \sum_n a_n\cos kL - m\sum_n k a_n \sin kL &= 0\label{sdlfkj}\tag{ii} \end{align} Each term in the summation of equation (\ref{sdlfkj}) must hold, giving \begin{align*} \rho_0 \cos kL - m k \sin kL &= 0\,, \end{align*} which in turn gives the transcendental equation \(kL\), \[\cot kL = \frac{mk}{\rho_0}\,.\] This tube with a mass at one end would not sound "good," in the sense that its eigenfrequencies are not evenly spaced, i.e., anharmonic, like the gamelan.

\(j\omega \rho_0 p + Z_n\partial p/\partial x = 0\) at \(x=L\) is called an impedance boundary condition. This boundary condition is a linear combination of the field variable and its gradient vanishing at the boundary.
What types of boundary conditions usually give rise to harmonic eigenfrequencies? [answer]

Boundary conditions in which either the field variable or its gradient vanishes generally give rise to harmonic eigenfrequencies. The previous example showed that anharmonic eigenfrequencies arise due to impedance boundary conditions.
What is the difference between resonance frequencies, eigenfrequencies, and natural frequencies? [answer]

Resonance is the infinite response (assuming no loss) of a system due to an external excitation. The frequency of that external excitation is called the resonance frequency. In contrast, eigenfrequencies are the frequencies at which a system vibrates, and they are found by solving the wave equation using orthogonal eigenfunctions. Eigenfrequencies depend on the shape, stiffness, and density of a system. Natural frequencies are synonymous with "eigenfrequencies."

In practice, eigenfrequencies coincide with resonance frequencies, and hence the three terms are often used interchangeably. But technically, resonance frequency refers to a driving frequency that coincides with an eigenfrequency, while the eigenfrequency is more closely related to the system.
Solve the wave equation for the transverse displacement \(\xi(x,t)\) \[\frac{\partial^2 \xi}{\partial x^2} - \frac{1}{c_0^2}\frac{\partial^2 \xi}{\partial t^2} = 0\] for \begin{align*} \xi(0,t)= 0\quad \text{and}\quad \xi(L,t) = \xi_0e^{j\omega_0 t}\,, \end{align*} the fixed-driven boundary conditions of a string. [answer]

See here for the solution, as well as some animations.
Derive an expression for the phase speed \(c_\text{ph}\), which is the speed of a point of constant phase. Write the phase as \(\Phi = \omega t - kx\) and set a differential element \(d\Phi\) equal to \(0\). [answer]

Since the phase speed is the speed of a point of constant phase, a differential element of phase \(d\Phi\) is constant: \[d\Phi = \frac{\partial\Phi}{\partial t}dt + \frac{\partial\Phi}{\partial x}dx =0\,.\] Solving for \(dx/dt\) and taking the derivatives of \(\Phi\) with respect to \(x\) and \(t\) gives the phase speed: \begin{align*} c_\text{ph} &= -\frac{\partial \Phi/\partial t}{\partial \Phi/\partial x} = \frac{\omega}{k} \end{align*}
☸ Derive an expression for the group speed. Write a signal in terms of its Fourier components, i.e., \( p(x,t)= \int_{-\infty}^{\infty} P(k)e^{j(\omega t-kx)}dk\). Take the first-order Taylor expansion of \(\omega(k)\) about \(k_0\), and denote \(\omega(k_0) = \omega_0\). Factor out from the integral \(e^{j(\omega_0 t-k_0x)}\), which represents a monochromatic wave with points of constant phase moving at \(\omega_0/k_0\). The remaining integral is the envelope of the wave packet. What is the speed of the wave packet? [answer]

The procedure above is followed: \begin{align*} p(x,t)&= \int_{-\infty}^{\infty} P(k)e^{j(\omega t-kx)}dk\\ &=\int_{-\infty}^{\infty} P(k)e^{j\{[\omega_0 + \frac{\partial \omega}{\partial k}\big\rvert_{k_0}(k-k_0)]t-kx\}}dk\\ &=e^{j(\omega_0t-k_0x)}\int_{-\infty}^{\infty} P(k)e^{j[\frac{\partial \omega}{\partial k}\big\rvert_{k_0}(k-k_0)t-(k-k_0)x]}dk\\ &=e^{j(\omega_0t-k_0x)}\int_{-\infty}^{\infty} P(k)e^{j[(k-k_0)\frac{\partial \omega}{\partial k}\big\rvert_{k_0}t-(k-k_0)x]}dk\\ &=e^{j(\omega_0t-k_0x)}\int_{-\infty}^{\infty} P(k)e^{j(k-k_0)\big(\frac{\partial \omega}{\partial k}\big\rvert_{k_0}t - x\big)}dk\\ \end{align*} The first factor outside the integral is a monochromatic wave with points of constant phase moving at \(\omega_0/k_0\). Meanwhile, the remaining integral is the envelope of the wave packet, traveling at group speed \[c_\text{gr} = \frac{\partial \omega}{\partial k}\bigg\rvert_{k_0}.\] The only assumption made in this derivation is that the wave packet is fairly narrowband, such that the first-order Taylor expansion of \(\omega(k)\) suffices.
At what speed does energy in a wave travel: the phase speed or the group speed? [answer]

Wave energy travels at the group speed. Thus the phase speed can be infinite, while the group speed is bounded by the speed of light.
On a plot of \(\omega\) vs \(k\), the slope of what line gives the phase speed? The slope of what line gives the group speed? [answer]

The slope of the secant line connecting the origin \((0,0)\) to a point \((k, \omega)\) is the phase speed. The slope of the tangent line at \((k, \omega)\) is the group speed.
The illustration below shows ocean waves traveling at various angles from the \(y\)-axis, which is parallel to the beach. For wave propagation toward the beach, i.e., in the \(x\)-direction, qualitatively describe what the phase speed and group speed correspond to. Without performing calculations, rank the group and phase speeds of the three sets of ocean waves. Then quantitatively provide expressions for the phase speed and group speed in the \(x\)-direction in terms of the ambient wave speed \(c\) and the angle \(\theta\). [answer]

Qualitatively: The phase speed is the apparent speed with which one wavefront sweeps along the \(x\)-axis, while the group speed is the component of the velocity \(c\) along the \(x\)-axis. For example, the phase speed of the ocean waves traveling at \(90^\circ\) with respect to the \(y\)-axis is the ambient wave speed \(c\) because its wavefronts sweep along the the \(x\)-axis at the speed at which the wave travels, and the group speed is also \(c\) because the wave motion is purely in the \(x\)-direciton. Meanwhile, the phase speed of the ocean waves traveling at \(0^\circ\) with respect to the \(y\)-axis is infinite because its wavefronts sweep along the the \(x\)-axis infinitely fast, while the group speed is also \(0\) because the wave motion has no component in the \(x\)-direction. The waves traveling at \(45^\circ\) have a phase speed larger than \(c\) but less than \(\infty\), and a group speed less than \(c\) but greater than \(0\). In summary, \(c = c^{90^\circ}_\text{ph} < c^{45^\circ}_\text{ph} < c^{0^\circ}_\text{ph} = \infty\), and \(0 = c^{0^\circ}_\text{gr} < c^{45^\circ}_\text{gr} < c^{90^\circ}_\text{gr} = c\).

Quantitatively: The phase speed is the trace velocity, which the trace wavelength times the frequency, \[c_\text{ph} = \frac{c}{\sin\theta}\,,\] while the group speed is the component of the velocity along the \(x\)-axis, \[c_{\text{gr}} = c\sin\theta\,.\]

More questions on phase speed and group speed follow in section 12.

Chapter 7: Horns

Of the continuity, momentum, and mass equations, which is/are adjusted to account for the changing cross-sectional area of a horn? [answer]

The momentum equation remains the same (though it takes several lines of algebra and the insertion of the continuity equation to show this). The state equation more obviously remains the same. The continuity is the only equation that ends up requiring an extra term. Repeating the derivation for the 1D continuity equation presented in chapter 1 while letting \(S=S(x)\) gives \[\frac{\partial \rho}{\partial t} + \frac{S'}{S}\rho u + \frac{\partial (\rho u)}{\partial x}= 0\,.\] Linearizing and combining the equations of continuity, momentum, and state results in the Webster horn equation, \begin{align*} \frac{\partial^2 p }{\partial x^2} + \frac{dS/dx}{S}\frac{\partial p}{\partial x} = \frac{1}{c_0^2}\frac{\partial^2 p}{\partial t^2}\,. \end{align*}
Obtain the phase speed for the exponential horn, in which \(S = S_0e^{mx}\). Identify the cutoff frequency. How does the magnitude of the solution grow? How could this growth be alternatively predicted from the conservation of energy? [answer]

Inserting \(S=S_0e^{mx}\) into the Webster horn equation gives \begin{align*} \frac{\partial^2 p }{\partial x^2} + m \frac{\partial p}{\partial x} = \frac{1}{c_0^2}\frac{\partial^2 p}{\partial t^2}\,. \end{align*} A solution proportional to \(e^{j(\omega t-kx)}\) is sought, giving \begin{align*} -k^2 - jkm &= -\frac{\omega^2}{c_0^2}\\ k^2 + jkm -k_0^2 &=0\\ \implies k &= -j\frac{m}{2} \pm \frac{\omega}{c_0}\sqrt{1-(m/2k_0)^2} \end{align*} The phase speed is found by taking the real part of the above and solving for \(\omega/k\): \begin{align*} c_\text{ph} = \frac{\omega}{k} = \frac{c_0}{\sqrt{1-(m/2k_0)^2}} \end{align*} Writing \(k_0 = \omega/c_0\) gives \(c_\text{ph} = \frac{c_0}{\sqrt{1-(mc_0/2\omega)^2}} = \frac{c_0}{\sqrt{1-(mc_0/4\pi f)^2}}\). The cutoff frequency is identified to be \(f^{(c)}= mc_0/4\pi\), and the phase speed can therefore be written as \begin{align*} c_\text{ph} = \frac{c_0}{\sqrt{1-(f^{(c)}/f)^2}}\,. \end{align*}

By substituting the expression for \(k\) into the form of solution \(e^{j(\omega t-kx)}\), it is seen that the magnitude of the solution grows as \[|p| \propto e^{-mx/2}.\] This result could be derived by noting that the power, remains constant as the wave propagates through the horn: \begin{align*} W = IS\propto p_\text{rms}^2 S &= \text{constant}\\ \implies p_\text{rms} &\propto 1/\sqrt{S}\\ &\propto 1/\sqrt{e^{mx}}\\ |p|&\propto e^{-mx/2} \end{align*}
Using the expression for \(k\) found above, find the impedance \(Z = p/u = \omega\rho_0/k\) of the exponential horn. Where does \(p/u = \omega\rho_0/k\) come from? [answer]

Inserting \(k = -j\frac{m}{2} \pm \frac{\omega}{c_0}\sqrt{1-(m/2k_0)^2}\) into this expression for the impedance gives \begin{align*} Z &= \frac{\omega\rho_0}{-j\frac{m}{2} \pm \frac{\omega}{c_0}\sqrt{1-(mc_0/4\pi f)^2}}\\ &=\frac{2\pi f\rho_0}{-j\frac{m}{2} \pm \frac{\omega}{c_0}\sqrt{1-(f^{(c)}/f)^2}}\\ &=\frac{\rho_0}{-j\frac{m}{4\pi f} \pm \frac{1}{c_0}\sqrt{1-(f^{(c)}/f)^2}}\\ &=\frac{\rho_0c_0}{-j\frac{mc_0}{4\pi f} \pm \sqrt{1-(f^{(c)}/f)^2}}\\ &=\frac{\rho_0c_0}{-jf^{(c)}/f \pm \sqrt{1-(f^{(c)}/f)^2}}\\ \end{align*} The rectangular form of the impedance is \begin{align*} Z &= \frac{\rho_0c_0}{-jf^{(c)}/f \pm \sqrt{1-(f^{(c)}/f)^2}}\frac{jf^{(c)}/f \pm \sqrt{1-(f^{(c)}/f)^2}}{jf^{(c)}/f \pm \sqrt{1-(f^{(c)}/f)^2}}\\ &=\rho_0c_0 \bigg[jf^{(c)}/f \pm \sqrt{1-(f^{(c)}/f)^2}\bigg] \end{align*}
☸ Calculate the input power \(W_\text{in} = S_0 I=S_0\langle pu \rangle = \frac{1}{2}S_0 \Re (pu^*)\) from a velocity source of an exponential horn, and write the result in terms of the power in a plane waveguide of constant cross section \(W_0 = \frac{1}{2}\rho_0c_0 S_0 u_0^2\). How does this result change for a pressure source? [answer]

The power for the velocity source is \begin{align*} W_\text{in}&= \frac{1}{2}S_0 \Re (pu^*)\\ &=\frac{1}{2}S_0 |u|^2\Re (Z_\text{in})\\ &= \frac{W_0}{\rho_0c_0}\Re (Z_\text{in})\\ &= W_0 \sqrt{1-(f^{(c)}/f)^2} \end{align*} where \(|u|^2=u_0^2\).

Meanwhile, for a pressure source, \(W_0 = \frac{1}{2\rho_0c_0} S_0 p_0^2\). The power for the pressure source is \begin{align*} W_\text{in}&= \frac{1}{2}S_0 \Re (pu^*)\\ &=\frac{1}{2}S_0 |p|^2\Re (1/Z_\text{in})\\ &= W_0\rho_0c_0\Re (1/Z_\text{in})\\ &= W_0 \sqrt{1-(f^{(c)}/f)^2} \end{align*} where \(|p|^2=p_0^2\). It is rather remarkable that the power exerted by an exponential horn driven by a pressure source equals the power exerted by the horn driven by a velocity source. This invariance is unique to exponential horns.
What is the definition of the transmission factor \(\text{TF}\)? Calculate \(\text{TF}\) for the exponential horn for a velocity source and a pressure source. [answer]

The transmission factor is defined as \begin{align*} \text{TF}&= \frac{W_\text{in}}{W_0} \end{align*} For the exponential horn, the previous result is used, giving \(\text{TF} = \sqrt{1-(f^{(c)}/f)^2}\) for above the cutoff frequency, and \(0\) for below the cutoff frequency. This is the transmission factor for both the pressure source and the velocity source.
For a conical horn, the horn height grows linearly with distance, i.e., \(y = mx\). Write the Webster horn equation for the conical horn. Read off the solution to this partial differential equation. What is the impedance of this horn in rectangular form? [answer]

The cross-sectional area is \(S(x) = \pi x^2\), and thus \(d S/dx = 2\pi x\). Thus the Webster horn equation \begin{align*} \frac{\partial^2 p}{\partial x^2} + \frac{2}{x}\frac{\partial p}{\partial x} = \frac{1}{c_0^2}\frac{\partial^2 p}{\partial t^2}\,. \end{align*} The solution to this PDE is immediately read off as spherical waves in \(x\).

The input impedance of this horn is given by the spherical wave impedance in rectangular form found in chapter 1, where \(x=x_0\) corresponds to the location of the mouth: \[Z_\text{in}/\rho_0 c_0 = \frac{jk_0x_0 + (k_0x_0)^2}{1 +( k_0x_0)^2}\]
Find the input power \(W_\text{in}\) from a velocity source of a conical horn, and write the result in terms of the power in a plane waveguide of constant cross section \(W_0 = \frac{1}{2}\rho_0c_0 S_0 u_0^2\). How does this result change for a pressure source? Also find the transmission factor for both velocity and pressure sources. [answer]

The power for the velocity source is \begin{align*} W_\text{in}&= \frac{W_0}{\rho_0c_0}\Re (Z_\text{in})\\ &= W_0 \frac{(k_0x_0)^2}{1 +( k_0x_0)^2}\\ \implies \text{TF} &= \frac{(k_0x_0)^2}{1 +( k_0x_0)^2} \end{align*} Meanwhile, the power for the pressure source is \begin{align*} W_\text{in}&= W_0\rho_0c_0\Re (1/Z_\text{in})\\ &= W_0 \\ \implies \text{TF} &= 1 \end{align*}
Does the conical horn give rise to dispersion? For what frequencies can the conical horn be used? At low frequencies, is it better to use a conical horn driven by a pressure source or a velocity source? [answer]

The conical horn does not give rise to dispersion, because \(d\omega/dk =1\) for spherical waves. The conical horn can be used for all frequencies. At low frequencies, it is better to use a conical horn driven by a pressure source, because \(\text{TF} = 1\) for all frequencies.
What is an advantage and a disadvantage of the catenoidal horn, which has the height profile \(y(x)= y_0\cosh \frac{x}{h}\). [answer]

The catenoidal horn, which must be treated using the WKB method (not covered in class) has the advantage of having vanishing slope at \(x=0\), which allows for it to be joined smoothly to a tube of radius \(y_0\). This eliminates reflections from the junction of the tube to the horn. A disadvantage is that the horn, like an exponential horn, has a cutoff frequency, below which the horn does not propagate waves.

Chapter 8: Sound in stratified media

What is primarily responsible for the stratification of the atmosphere? In which governing equation does this manifest? [answer]

Gravity is primarily responsible for the stratification of the atmosphere. It appears on the right-hand side of the momentum equation, as seen in the following problem.
Simplify the 1D momentum equation with a body force \(\rho (u_t + uu_z)+ P_z = -\rho g\) for a motionless fluid, i.e., \(u=0, P=p_0, \rho=\rho_0\), to obtain \begin{equation}\label{gravity} \frac{dp_0}{dz} = -\rho_0 g\,. \tag{8} \end{equation} What are two different assumptions on \(\rho_0\) that allow for simple solutions of equation (\ref{gravity})? [answer]

Setting \(u=0, P=p_0, \rho=\rho_0\) in the 1D momentum equation with a body force gives \begin{align*} \rho_0 (0) + (p_0)_z &= -\rho_0 g\\ \implies \frac{dp_0}{dz} &= -\rho_0 g\,. \end{align*}
One simple way to solve equation (\ref{gravity}) is to assume \(\rho_0 = \) constant (see problem 3). The next simplest approach is to consider an atmosphere in which \(T_0\) is constant, and thus by the ideal gas law \(\rho_0 \propto p_0\) (see problem 4).
Assume that the density is constant i.e., \(\rho_0 \neq \rho_0(z)\), and thus integrate equation (\ref{gravity}). Let \(\bar{p}_0 = p_0(z=0)\) be the sea-level pressure. What is the scale height of the atmosphere? Use the adiabatic relation \(c_0^2 = \gamma \bar{p}_0/\rho_0\) to eliminate density from the final expression. [answer]
Integrating \(dp_0/dz = -\rho_0 g\) over \(z\) gives \begin{align*} p_0 &= \bar{p}_0-\rho_0 g z\,. \end{align*} The scale height is the height \(H\) at which the atmosphere terminates: \(p_0=0 =\bar{p}_0-\rho_0 g H \), which gives \[H = \frac{\bar{p}_0}{\rho_0 g} = \frac{c_0^2}{\gamma g}\]
Next assume that the temperature is \(T_0\) at all heights. Why is "isothermal" not the best word choice for such an atmosphere? Combine the ideal gas law \(\rho_0 = p_0/RT_0 = \gamma p_0/c_0^2\) with the definition of the scale height \(c_0^2 = H\gamma g\) and eliminate \(\rho_0\) in equation (\ref{gravity}), and thus obtain \begin{equation}\label{integrateher} \frac{dp_0}{dz} = -\frac{p_0}{H}\,. \tag{9} \end{equation} Solve equation (\ref{integrateher}) for \(p_0\). [answer]

"Isothermal" is poor word choice because the sound propagation is still adiabatic in this model. Combining \(\rho_0 = \gamma p_0/c_0^2\) with the definition of the scale height \(c_0^2 = H\gamma g\) gives \begin{equation}\label{rho0}\tag{i} \rho_0 = \frac{p_0}{gH}. \end{equation} Using the above to eliminate \(\rho_0\) in equation (\ref{gravity}) gives \[\frac{dp_0}{dz} = -\frac{p_0}{H},\] the solution of which is \(p_0 = \bar{p}_0e^{-z/H}\). Combination with equation (\ref{rho0}) gives the same profile for the ambient density, \(\rho_0 = \bar{\rho}_0e^{-z/H}\).
Linearize the 1D continuity equation, \(\partial\rho/\partial t + (\rho u)_z = 0\), for the case of a variable ambient density \(\rho_0= \rho_0(z)\). [answer]

Writing \(\rho = \rho_0(z) + \rho'\) gives \begin{align} \frac{\partial}{\partial t}[\rho_0(z) + \rho'] + \frac{\partial}{\partial z}[(\rho_0(z) + \rho')u] &= 0\notag\\ \frac{\partial \rho'}{\partial t} + u\frac{\partial \rho_0(z)}{\partial z} + \rho_0(z)\frac{\partial u}{\partial z} &= 0\tag{ii}\label{conters} \end{align}
Linearize the 1D momentum equation with a body force, \(\rho(\partial u /\partial t + u\partial u/\partial z) + \partial P/\partial z = -\rho g\), where \(\rho_0= \rho_0(z)\). Simplify the result by invoking equation (\ref{gravity}) [answer]

Writing \(P = p_0(z) + p\) gives \begin{align*} [\rho_0(z) + \rho']\bigg[\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial z}\bigg] + \frac{\partial }{\partial z}[p_0(z) + p] &= -[\rho_0(z)+\rho']g\\ [\rho_0(z) + \rho']\bigg[\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial z}\bigg] + \frac{\partial p_0(z)}{\partial z} + \frac{\partial p}{\partial z} &= -\rho_0(z)g - \rho'g \end{align*} Since by equation (\ref{gravity}) \(dp_0/dz = - \rho_0(z) g\), the above reduces to \begin{align*} [\rho_0(z) + \rho']\bigg[\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial z}\bigg] + \frac{\partial p}{\partial z} &= - \rho'g \end{align*} Linearization gives \begin{align} \rho_0(z)\frac{\partial u}{\partial t} + \frac{\partial p}{\partial z} &= - \rho'g\,.\label{momers}\tag{iii} \end{align}
In a stratified medium, what assumption is made about the local entropy? Use this assumption to simplify the state equation \[\frac{DP}{Dt} = \bigg(\frac{\partial P}{\partial \rho}\bigg)_s \frac{D\rho}{Dt} + \bigg(\frac{\partial P}{\partial s}\bigg)_\rho \frac{Ds}{Dt}\,,\] and recall that \(Df/Dt = \partial f/\partial t + u\partial f/\partial z\) for an arbitrary quantity \(f\). [answer]

In a stratified medium, the entropy of a given particle is assumed to remain constant even though the entropy may vary from particle to particle, i.e., \(Ds/Dt =0\). The state equation becomes \begin{align} \frac{DP}{Dt} &= c^2 \frac{D\rho}{Dt}\notag\\ \frac{\partial P}{\partial t} + u\frac{\partial P}{\partial z} &= c^2 \frac{\partial\rho}{\partial t} + c^2u\frac{\partial p}{\partial z}\notag\\ \frac{\partial }{\partial t}[p_0(z) + p] + u\frac{\partial }{\partial z}[p_0(z) + p] &= c_0^2 \frac{\partial}{\partial t}[\rho_0(z) + \rho'] + c_0^2u\frac{\partial }{\partial z}[\rho_0(z) + \rho']\notag\\ \frac{\partial p}{\partial t} + u \frac{\partial p_0(z) }{\partial z} &= c_0^2 \frac{\partial \rho'}{\partial t} + c_0^2 u\frac{\partial \rho_0(z)}{\partial z}\label{staters}\tag{iv} \end{align}
Equation (\ref{conters}) is used to eliminate density from the right-hand side of equation (\ref{staters}), giving \(\partial p/\partial t + u\partial p_0/\partial z = -c_0^2\rho_0 \partial u/\partial z\). Using equation (\ref{gravity}) to eliminate the static pressure gradient on the left-hand side gives \(\partial p/\partial t - g\rho_0 u = -c_0^2\rho_0 \partial u/\partial z\). Taking the \(z\) derivative with respect to this result gives \begin{equation}\label{combiners}\tag{v} \frac{\partial^2 p}{\partial z\partial t} - g\frac{\partial}{\partial z}\bigg[\rho_0 \frac{\partial u}{\partial z}\bigg] = -\frac{\partial}{\partial z}\bigg[c_0^2\rho_0 \frac{\partial u}{\partial z}\bigg]\,. \end{equation} Meanwhile, rearranging equation (\ref{momers}) and taking the time derivative gives \(\partial^2 p/\partial z\partial t + g\partial\rho'/\partial t = -\rho_0 \partial^2 u/\partial t^2\). Combining this equation with equation (\ref{conters}) to eliminate \(\partial\rho'/\partial t\) gives \begin{equation}\label{combiners2}\tag{vi} \frac{\partial^2 p}{\partial z\partial t} - g\frac{\partial}{\partial z}(\rho_0 u) = -\rho_0\frac{\partial^2 u}{\partial t^2}\,. \end{equation} Subtract equation (\ref{combiners}) from equation (\ref{combiners2}) to obtain \begin{equation}\label{horny}\tag{10} \frac{\partial^2 u}{\partial z^2} + \frac{\partial (\rho_0c_0^2)/\partial z}{\rho_0c_0^2}\frac{\partial u}{\partial z} - \frac{1}{c_0^2}\frac{\partial^2 u }{\partial t^2} = 0, \end{equation} the wave equation for plane waves in an inhomogeneous medium. [answer]

Using subscripts to denote partial derivatives, the subtraction yeilds \begin{align*} -\rho_0 u_{tt} + \rho_0 c_0^2 u_{zz} - (\rho_0 c_0^2)_z u_z &=0\,. \end{align*} Rearranging and dividing by \(\rho_0c_0^2\) gives \begin{align*} u_{zz} + \frac{(\rho_0 c_0^2)_z}{\rho_0 c_0^2} u_z -c_0^{-2} u_{tt} &=0 \end{align*}
In what limit does equation (\ref{horny}) recover \(\frac{\partial^2 u}{\partial z^2} - \frac{1}{c_0}\frac{\partial^2 u }{\partial t^2}\)? How is \(\frac{\partial^2 u}{\partial z^2} - \frac{1}{c_0}\frac{\partial^2 u }{\partial t^2}\) different from the "normal" 1D wave equation? [answer]

The correct limit is the slowly varying or quasistatic limit \(\lambda \ll L\), i.e., the wave doesn't care about the variation in ambient density of characteristic length \(L\) over one wavelength \(\lambda\).

It is good to be able to show this. The following sort of argument is emphasized by Dr. Hamilton in all his classes. Let \(u\) be spatially and temporally harmonic. Then the orders of the quantities in equation (\ref{horny}) are \begin{align*} \frac{\partial u}{\partial z} &\sim -jku = \mathcal{O}(ku) = \mathcal{O}(u/\lambda)\\ \frac{1}{c_0^2}\frac{\partial^2 u}{\partial t^2} &\sim \frac{\omega^2}{c_0^2}u = \mathcal{O}(k^2u) = \mathcal{O}(u/\lambda^2)\\ \frac{d(\rho_0c_0^2)}{dz} &= \mathcal{O}(\rho_0c_0^2/L) \end{align*} So in terms of orders, equation (\ref{horny}) is \begin{align*} \mathcal{O}(u/\lambda^2) + \mathcal{O}(u/\lambda L) - \mathcal{O}(u/\lambda^2) =0 \end{align*} Dividing through by \(\mathcal{O}(u/\lambda^2)\) gives \begin{align*} \mathcal{O}(1) + \mathcal{O}(\lambda/L) - \mathcal{O}(1) =0 \end{align*} But \(\mathcal{O}(\lambda/L) = 0\), so the middle term of equation (\ref{horny}) is much smaller than the first and third terms, resulting in \[\frac{\partial^2 u}{\partial z^2} - \frac{1}{c_0}\frac{\partial^2 u }{\partial t^2}\,.\] In the above equation, note that \(c_0=c_0(z)\), whereas in the "normal" 1D wave equation for isotropic medium, \(c_0\) is a constant.
What is striking about equation (\ref{horny})? [answer]

Equation (\ref{horny}) is of the same form as the Webster horn equation, in which the bulk modulus \(\rho_0c_0^2\) plays the role of the cross-sectional area \(S\) of the horn. However, note that \(c_0\) is not necessarily a independent of \(z\), unlike for the case of the horn.
What kind of atmosphere renders equation (\ref{horny}) identical in form to the Webster horn equation for an exponential horn? [answer]

In question 4 above, it was found that for a constant temperature \(T_0\) at all heights, \(c_0\) is constant and \(\rho_0(z) = \bar{\rho}_0e^{-z/H}\). In that case, equation (\ref{horny}) becomes \begin{align*} u_{zz} + \frac{1}{H} u_z - \frac{1}{c_0^2} u_{tt} &=0 \end{align*}
Insert the trial solution \(u = \bar{u}_0 \exp[j(\omega t - kz)]\) into \(u_{zz} + \frac{1}{H} u_z - \frac{1}{c_0^2} u_{tt} =0\) to obtain \(|u(z)|\), where \(\bar{u}_0\) is the particle velocity amplitude at sea level. What is remarkable about this result? Derive this result directly from the conservation of energy. [answer]

Inserting \(u = u_0 \exp[j(\omega t - kz)]\) into \begin{align*} u_{zz} + \frac{1}{H} u_z - \frac{1}{c_0^2} u_{tt} &=0 \end{align*} gives \begin{align*} -k^2 + \frac{jk}{H} + k_0^2 &=0\,. \end{align*} Solving for \(k\) gives \[k = \frac{j}{2H} \mp \frac{1}{2H}\sqrt{1-(2kH)^2}\,,\] and the magnitude of the trial solution becomes \[|u| = \bar{u}_0\exp{(z/2H)}\,.\] What is remarkable about this result is that it predicts the exponential growth of sound without violating the conservation of energy.

To derive this result directly from the conservation of energy, note that the intensity is constant, so \begin{align*} \langle I \rangle = \text{constant} &= \rho_0 c_0 u_\text{rms}^2 \\ &=\bar{\rho}_0 e^{-z/H} c_0 u_\text{rms}^2 \,. \end{align*} Since \(c_0\) and \(\bar{\rho}_0\) are constants, \(u_\text{rms}^2\propto e^{z/H} \) so \(u_\text{rms} \propto e^{z/2H}\).
Water is most dense at \(4^\circ \text{ C}\). What is the temperature of the deep ocean? [answer]

\(4^\circ \text{ C}\), which is not at all an intuitive result to me.

In fact this reminds me of questions like, "Mary has three apples and John has two oranges. What is the mass of the sun?"
Explain the various features in the ocean sound speed profile.
Adapted from figure 8.2(b) from Fundamentals of Physical Acoustics by David T. Blackstock
List any names for the features labeled in the figure. [answer]

Starting at the surface, the sound speed profile is fairly constant. This is because the surface layer of the ocean is fairly mixed; thus the temperature is constant throughout that layer. The slight positive slope in this layer is due to the increasing depth.

Below the surface layer is the so-called "thermocline." In this layer, the sound speed gradient is negative due to the drop in temperature, which is due to the attenuation of sunlight (which warms the water) in the \(z\) direction. However, the sound speed's dependence on temperature weakens as depth increases, and its dependence on depth begins to be felt.

At 1 km, the effect of dropping temperature and increasing depth strike a balance (which depends on salinity), and the sound speed attains a minimum. This minimum establishes the SOFAR channel.

As found in the previous question, water is \(4^\circ \text{ C}\) for the deep ocean, i.e., temperature is constant. Therefore, going deeper than this minimum, the sound speed profile is dominated by increasing depth.
For what frequencies is ray theory a good approximation? What are some other assumptions made when treating sound as rays? How does the amplitude of sound in a ray depend on the cross-sectional area of a ray? [answer]

Ray theory works for \(ka \to \infty\). The main assumption (really, the same thing as \(ka \to \infty\)), is that diffraction is neglected. Also, since the acoustic power in a ray is assumed to be constant, caustics (the intersection of rays) cannot be handled.

Rays are assumed to conserve power as they propagate. That is, \(W = IS \propto p_\text{rms}^2S = \text{ constant}\). Thus \(p_\text{rms} \propto |p| \propto 1/\sqrt{S}\), as is the case for horns.
How are angles defined in ray theory? Write Snell's law in this convention. [answer]

Angles are measured from grazing incidence, i.e., \(\theta = 0^\circ\) for grazing incidence and \(\theta = 90^\circ\) for normal incidence. Snell's law therefore reads \[\frac{\cos\theta_1}{c_1} = \frac{\cos \theta_2}{c_2}\,.\]
Since Snell's law applies everywhere in a stratified medium, \(\cos(\theta)/c(\theta)\) is a constant. Find an expression for \(dc/d\theta\). [answer]

Differentiating \(\cos(\theta)/c(\theta) = \text{ constant}\) gives \begin{align*} \frac{d}{d\theta}\frac{\cos\theta}{c(\theta)}&= 0\\ -\frac{\sin\theta}{c(\theta)} - \frac{\cos\theta}{c^2(\theta)}\frac{dc}{d\theta} &= 0\\ \implies \frac{dc}{d\theta}&=- \frac{\sin\theta}{c(\theta)}\frac{c^2(\theta)}{\cos\theta}\\ &=-\frac{c\sin(\theta)}{\cos\theta} \end{align*}
☸ Define the sound speed gradient to be \(g\equiv dc/dz\). Define the radius of curvature \(R_c \equiv ds/d\theta\). Use the chain rule, the definition of the sound speed gradient, and the differential form of Snell's law \(dc/d\theta\) from the previous problem, to express \(R_c \) in terms of \(\theta\), \(g\), and \(c\). Note that \(dz/ds = \sin(\theta)\). [answer]

\begin{align*} R_c&= \frac{ds}{d\theta} = \frac{ds}{dz}\frac{dz}{dc}\frac{dc}{d\theta}\\ &=-\frac{1}{\sin\theta}\frac{1}{dc/dz}\frac{c\sin(\theta)}{\cos\theta}\\ &=-\frac{1}{g}\frac{c}{\cos\theta}\\ \end{align*}
If \(g<0\), what is the sign of \(R_c\)? In that case, does the ray bend toward or away from the surface? What about for \(g>0\)? [answer]

If \(g<0\), \(R_c\) is positive, so the ray bends away from the surface. The opposite behaviour occurs for \(g>0\). The way I remember this is by noting that sound bends in the direction of the slower medium (see chapter 5, problem 6 above).
The figure below is adapted from Blackstock's figure 8.8. It shows that a ray in a linear sound speed profile traverses a depth and range of \begin{align} \Delta z &= R_c(\cos\theta_i - \cos\theta)\label{skippy} \tag{11}\\ \Delta r &= R_c(\sin\theta - \sin\theta_i)\,. \label{skippy2} \tag{12} \end{align} 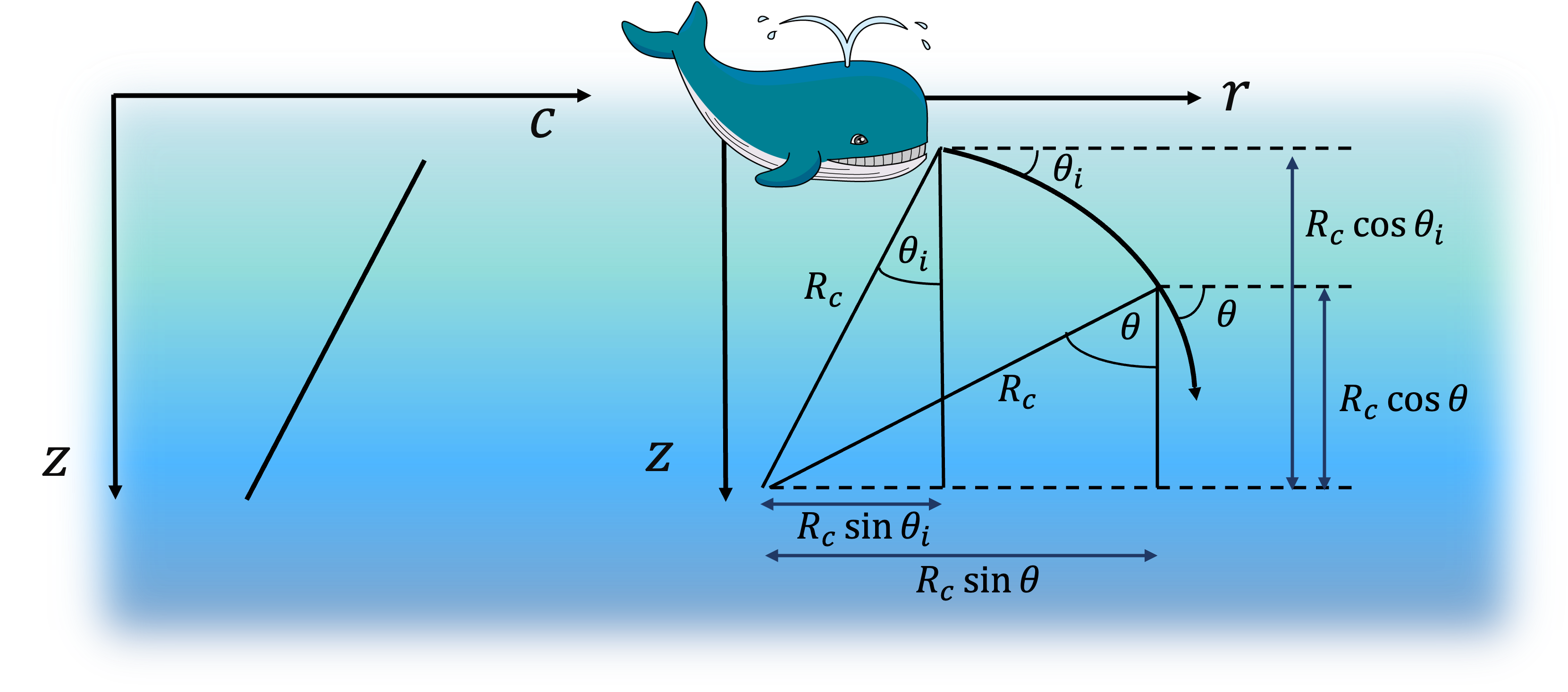Find the distance from the source to the vertex by setting \(\theta=0\) and using the expression for \(R_c\) found in problem 18. [answer]

\begin{align*} \Delta z_v &= R_c(\cos\theta_i - 1)= -\frac{1}{g}\frac{c}{\cos\theta_i}(\cos\theta_i - 1) = \frac{c}{g}\frac{1-\cos\theta_i}{\cos\theta_i} \\ \Delta r_v &= -R_c\sin\theta_i = \frac{c}{g}\frac{\sin\theta_i}{\cos\theta_i} = \frac{c}{g}\tan\theta_i \end{align*}
For \(dc/dz = g>0\), it is possible for the sound rays to bounce (or "skip", hence \(\theta_s\)) off the the surface, as shown in the figure below adapted from Blackstock's figure 8.10:
In this case, setting \(\theta_i=0\) and using equations (\ref{skippy}) and (\ref{skippy2}), \begin{align*} -d &= R_c(1 - \cos\theta_s)\\ r_0 &= R_c \sin\theta_s\,. \end{align*} Solve for \(r_0\), which is called the cycle distance. [answer]

First solve for \(\cos\theta_s\) and \(\sin\theta_s\): \begin{align*} 1+\frac{d}{R_c} &= \cos\theta_s\\ -\frac{r_0}{R_c} &= \sin\theta_s\,. \end{align*} Square the above equations and add: \begin{align*} (1+ d/R_c)^2 + (r_0/R_c)^2 &= 1\\ 1+ 2d/R_c + (d/R_c)^2 + (r_0/R_c)^2 &=1\\ 2d/R_c + (d/R_c)^2 + (r_0/R_c)^2 &=0 \end{align*} Solve for \(r_0\): \begin{align*} r_0 &= R_c \sqrt{-2d/R_c - (d/R_c)^2}\\ &= \sqrt{-2dR_c - d^2} \end{align*}
Is it possible for a ray to execute a closed trajectory, i.e., make a loop? Why are or why not? [answer]

It is not possible for a ray to execute a closed trajectory. While mathematically a ray follows a circular trajectory in a constant sound speed gradient, the model falls apart by the time the ray is traveling vertically (in the \(z\) direction, for the examples considered in the above problems). This is because Snell's law for normal incidence results in refraction at normal incidence. Therefore, once the ray is headed in the \(z\) direction, it will go down until it hits the ocean floor.
Obtain the phase speed and group speed given the dispersion relation \(k = \omega n(\omega)/c_0\). [answer]

The phase speed is simply \[c_\text{ph} = \frac{\omega}{k} = \frac{c_0}{n(\omega)}\,.\] To find the group speed, take \(dk/d\omega\) \begin{align*} \frac{dk}{d\omega} = \frac{1}{c_0} [n(\omega) + \omega n'(\omega) ] \end{align*} and invert for \(d\omega/dk\): \begin{align*} \frac{d\omega}{dk} = \frac{c_0}{n(\omega) + \omega n'(\omega)}\,. \end{align*}

Chapter 9: Absorption and dispersion

Acoustics is the continuum approximation of sound in fluid media, which in reality consists of the compressions and rarefactions of vast ensembles of molecules. What must the mean free path of these molecules be for sound to propagate? Note that the mean free path is the average distance traveled by a molecule before hitting another molecule. [answer]

This is a point made by R. P. Feynman in his lecture "Sound and the Wave Equation." For sound to exist, the mean free path must be much less than a wavelength. Otherwise, the molecular behaviour is diffusive.
What are the units of the absorption coefficient \(\alpha\)? How does one convert between \(\text{SPL}\) and \(\alpha\)? [answer]

\(\alpha\) has units of \(\text{neper } \text{meters}^{-1}\). In fact, nepers are dimensionless! (How ridiculous). To convert from \(\text{SPL}\) to \(\alpha\), consider the form of an attenuating wave, \(|p| = A e^{-\alpha x}\). Then, \begin{align*} \text{SPL} &= 20 \log_{10} \frac{A/\sqrt{2}}{p_\text{ref}}\\ &= 20 \log_{10} \frac{A\,e^{-\alpha x}/\sqrt{2}}{p_\text{ref}}\\ &= 20 \log_{10} \frac{A/\sqrt{2}}{p_\text{ref}} + 20\log_{10} e^{-\alpha x}\\ &= \text{SPL}_0 + 20\log_{10} e^{-\alpha x}\\ &= \text{SPL}_0 - 8.686 \alpha x\,, \end{align*} where \(\text{SPL}_0\) is the sound pressure level at the source \(x=0\).
The linearized viscous wave equation in 1D is found by combining the linearized continuity, momentum, and state equations (the momentum equation being the only one with modification from the "classic" wave equation). It is given by \[\frac{\nu \tilde{V}}{c_0^2} u_{xxt} + u_{xx} - \frac{1}{c_0^2} u_{tt} = 0,\] where \(\nu\) is the kinematic viscosity coefficient and \(\tilde{V}\) is the viscosity number. Derive the attenuation coefficient, defining \(\delta_v = \omega \nu/c_0^2 \ll 1\). Is the medium dispersive? [answer]

Let \(u\, \propto \, e^{j(\omega t - k(\omega)x)}\). Substitution into the viscous wave equation gives \begin{align*} -j\omega k^2 \frac{\nu \tilde{V}}{c_0^2} -k^2 + \frac{\omega^2}{c_0^2} &= 0 \end{align*} Solve for \(k\): \begin{align*} k^2 (1 + j\omega{\nu \tilde{V}}/{c_0^2}) &= {\omega^2}/{c_0^2}\\ k^2 &= \frac{{\omega^2}/{c_0^2}}{1 + j\omega{\nu \tilde{V}}/{c_0^2}}\\ k &= \frac{\omega}{c_0} (1 + j\omega{\nu \tilde{V}}/{c_0^2})^{-1/2}\\ k &= \frac{\omega}{c_0} (1 + j \delta_v \tilde{V})^{-1/2} \end{align*} Since \(\delta_v \ll 1\), the binomial expansion is used, giving \begin{align*} k &= \frac{\omega}{c_0} (1 - j \delta_v \tilde{V}/2)\\ &= \frac{\omega}{c_0} - \frac{j\omega \delta_v\tilde{V}}{2} \end{align*} The attenuation coefficient is identified as \(\alpha = -\Im\, (k) = \omega \delta_v \tilde{V}/2c_0\), or reinstating \(\delta_v = \omega \nu/c_0^2\), \[\alpha_\text{v} = \frac{\omega^2 \nu \tilde{V}}{2c_0^3} \,.\] Meanwhile, note that the phase speed is \(c^{\text{ph}} = \omega/\Re\, (k) = c_0\). Thus the medium is non-dispersive (because \(\delta_v\ll 1\)).
The linearized wave equation for a thermally conducting fluid is found by combining the linearized continuity, momentum, and state equations (the state equation this time being the one with modifications). It is given by \[\frac{\kappa}{\rho_0 C_p} \bigg[u_{xx} -\frac{\gamma}{c_0^2}u_{tt}\bigg]_{xx} - \bigg[u_{xx} - \frac{1}{c_0^2}u_{tt}\bigg]_t = 0\,,\] where \(\kappa \) is the heat conduction coefficient and \(C_p\) is the specific heat at constant pressure. As a zeroth-order approximation, show that this equation reduces to the ''ordinary wave equation'' when the thermal conduction of the fluid is negligible. Then as a first-order approximation, approximate \(u_{xx}\) in the first term as \(-u_{tt}/c_0^2\) and integrate over time. Compare the above approximation of the thermally conducting wave equation to the viscous wave equation and read off the attenuation coefficient. [answer]

Zeroth order approximation. For \(\kappa/C_p\to 0\), the given equation (upon integration over \(t\)) gives the ''ordinary wave equation.''

First order approximation. Replacing \(u_{xx}\) in the first term as \(-u_{tt}/c_0^2\) gives \begin{align*} \frac{\kappa}{\rho_0 C_p} \bigg[-\frac{u_{tt}}{c_0^2} -\frac{\gamma}{c_0^2}u_{tt}\bigg]_{xx} - \bigg[u_{xx} - \frac{1}{c_0^2}u_{tt}\bigg]_t = 0 \end{align*} Integrating over time gives \begin{align*} \frac{(\gamma-1)\kappa}{\rho_0c_0^2C_p} u_{xxt} + u_{xx} - \frac{1}{c_0^2}u_{tt} = 0\,. \end{align*} This has the same form as the viscous wave equation which had the attenuation coefficient of \(\alpha = \frac{\omega^2 \nu \tilde{V}}{2c_0^3}\). Thus the attenuation coefficient for the thermally conducting wave equation is \begin{align*} \alpha_\text{th} = \frac{\omega^2 (\gamma-1)\kappa}{2\rho_0 c_0^3 C_p}\,. \end{align*} Similarly, it can be concluded that the thermally conducting wave equation describes non-dispersive wave motion.

See Blackstock's chapter 9, section B for a much more detailed derivation.
Having derived the attenuation coefficient for viscous fluids and thermally conducting fluids, derive the attenuation coefficient for thermoviscous fluids. What allows for the simple addition of these attenuation coefficients? [answer]

From Blackstock, footnote of page 300:
The validity of superposing the various contributions, e.g., putting \(\alpha_\text{total} = \alpha_1 + \alpha_2 + \alpha_3 + \dots\), is rarely discussed. In fact, superposition is in general not justified because although the various absorption mechanisms act mainly separately, they do have interactions with each other; see, for example, Sec. B.3. In practice, however ,the effect of each mechanism is normally so small that the interactions may be neglected, in which case superposition is justified.
Simply adding the previously found attenuation coefficients together gives \begin{align*} \alpha_\text{tv}&= \alpha_\text{v} + \alpha_\text{th}\\ &= \frac{\omega^2 \nu \tilde{V}}{2c_0^3} + \frac{\omega^2 (\gamma-1)\kappa}{2\rho_0 c_0^3 C_p}\\ &= \frac{\omega^2}{2c_0^3}\bigg[\nu \tilde{V} + \frac{(\gamma-1)\kappa}{\rho_0 C_p}\bigg] \end{align*} The above result can be rewritten in a number of ways (see Blackstock page 314); the main result, however, is that the thermoviscous absorption is quadratic in frequency.
Derive the 1D linearized wave equation for a relaxing medium, for which the equation of state is \(\tau (p- c_\infty^2 \rho')_t + (p -c_0^2 \rho') = 0,\) where \(\rho'\) is the perturbation density. Assess the behaviour for when the sound's period is much smaller than than the relaxation time (\(\omega\tau \to 0\)) and for when the sound's period is much larger than the relaxation time (\(\omega\tau \to \infty\)). [answer]

The linearized 1D continuity equation is \begin{align}\label{isldfkjsdf}\tag{i} \rho'_t + \rho_0 u_x= 0, \end{align} and the linearized 1D momentum equation is \begin{align}\label{iisldkfjsdlkfjasdlfj}\tag{ii} p_x + \rho_0 u_t = 0\,. \end{align} The particle velocity is eliminated by taking the time derivative of equation (\ref{isldfkjsdf}) and subtracting from the space derivative of equation (\ref{iisldkfjsdlkfjasdlfj}): \begin{align*} \rho'_{tt} = p_{xx}. \end{align*} Meanwhile the equation of state is differentiated twice w.r.t. \(t\): \begin{align*} \tau p_{ttt}- \tau c_\infty^2 \rho'_{ttt} + p_{tt} -c_0^2 \rho'_{tt} &= 0\,. \end{align*} The density is eliminated between \(\rho'_{tt} = p_{xx}\) and the above equation of state, giving the wave equation for a relaxing fluid: \begin{align*} \tau p_{ttt}- \tau c_\infty^2 p_{xxt} + (p_{tt} -c_0^2 p_{xx}) &= 0\,. \end{align*} The term in parentheses is simply the ''ordinary linear wave equation.''

To assess the low- and high-frequency limits, insert a harmonic test solution i.e., \(p \,\propto \,e^{j\omega t - jkx}\): \begin{align*} -j\omega^3\tau + j\omega \tau k^2 c_\infty^2 + (-\omega^2 + k^2 c_0^2 ) &= 0\\ j\omega\tau (-\omega^2 + k^2 c_\infty^2) + (-\omega^2 + k^2 c_0^2 ) &= 0 \end{align*} In the limit that \(\omega\tau \to 0\) (the sound's period is much larger than the relaxation time), the first term vanishes, resulting in wave propagation at \(c_0\). In this limit, the change in pressure and density is so slow that ''equilibrium is reestablished after each infinitesimal pressure change in the acoustical cycle'' (Blackstock page 318). That is to say, the relaxation mechanism happens basically instantaneously compared to the period of the wave, and thus the wave propagates oblivious to the reaction mechanism, and the sound travels at the ambient speed of sound propagation, \(c_0\), with the molecules relaxed for almost the entire time.

In the limit that \(\omega \tau \to \infty\) (the sound's period is much shorter than relaxation time) the first term dominates, resulting in wave propagation at \(c_\infty\). In this limit, the frequency of the sound wave is so high that the pressure and density much faster than the relaxation mechanism. Thus, over one period of sound, the molecules don't get the slightest chance to relax. They stay frozen in their ''anxious'' state.

Chapter 10: Spherical waves

Obtain the general solution to the wave equation in spherical coordinates. [answer]

See here for a video solution of the wave equation in spherical coordinates.
Every second-order ordinary differential equation has two linearly independent solutions. For example, \(y'' + k^2y=0\) has solutions \(\cos kx\) and \(\sin kx\). \(y'' - k^2y=0\) has solutions \(e^{kx}\) and \(e^{-kx}\). Bessel's equation has solutions \(j_n(kr)\) and \(n_n(kr)\). Why, then, does the solution of the spherical wave equation only contain one solution to Legendre's equation, \(P_n(\cos\theta)\) (or \(P^m_n(\cos\theta)\) in the most general case)? [answer]

This was discussed in the "Orthogonality and Special Functions" section of the math page: see problem 2. \(Q_n\) diverges at the poles and is therefore neglected in the solution to the Helmholtz equation, because most problems in acoustics involve \(\theta =0\) and \(\theta = \pi\).
Is it possible for multiple eigenfunctions to map to the same eigenfrequency? Is it possible for multiple eigenfrequencies to map to the same eigenfunction? Why or why not? [answer]

It is possible for multiple eigenfunctions to map to the same eigenfrequency. This is called degeneracy, as a student of quantum mechanics would know. For example, take the eigenfrequencies of sound in a cube is proportional to \(\sqrt{n^2 + m^2 + l^2}\), where \(n\), \(m\), and \(l\) are non-negative integers. The eigenfrequency corresponding to \(n= 1, m = 0, l=0\) equals that corresponding to \(n= 0, m = 1, l=0\), which in turn equals that corresponding to \(n= 0, m = 0, l=1\). The degeneracy for this lowest energy is thus \(3\). For the degeneracy of the next highest energy would be \(6\).

However, it is not possible for multiple eigenfrequencies to map to the same eigenfunction. In other words, it is not possible for one eigenfunction to correspond to multiple eigenfrequencies. One can employ a simple proof by contradiction. Suppose for a nontrivial \(\vec{x}\) that \(A\vec{x} = \lambda \vec{x}\) and \(A\vec{x} = \mu \vec{x}\), where \(\lambda \neq \mu\). Then by subtraction, \[0 = (\lambda-\mu)\vec{x}.\] Since \(\vec{x} \neq 0\), by the zero product property, \(\lambda-\mu = 0 \implies \lambda = \mu\). But this contradicts the assumption that \(\lambda \neq \mu\). Since the assumption led to a contradiction, the assumption must be false.

While the argument above has been written in the form of an eigenvalue problem of eigenvectors, eigenvalues, and matrices, it is identitical to the argument that would be made for eigenfunctions, eigenfrequencies, and linear differential operators. Simply replace \(\vec{x}\) above with \(p(\vec{r})\), \(\lambda\) and \(\mu\) with \(\omega_1\) and \(\omega_2\), and \(A\) with \(\nabla^2\). The argument then shows that one eigenfunction of the Helmholtz equation cannot map to multiple eigenfrequencies.
Let \(n\) be either \(r,\theta,\) or \(\psi\). How does one satisfy the boundary conditions if the \(n\)th surface is pressure-release? How does one satisfy the boundary conditions if the \(n\)th surface is rigid? [answer]

Pressure-release: The condition is simply that \(p\) evaluated at the surface \(n\) vanishes. That is, if the pressure-release surface is specified at a particular radius, \(p(r=a) = 0\); if the pressure-release surface is specified at a particular polar angle \(\theta_0\), \(p(\theta = \theta_0) = 0\); if the pressure-release surface is specified at a particular azimuthal angle \(\psi_0\), \(p(\psi = \psi_0) = 0\).

Rigid: The condition is that \(\partial p^{(n)}/\partial n = 0\). For example, if the rigid surface is specified at a particular radius, the condition is \(\partial p^{(r)}/\partial r = 0\); if the rigid surface is specified at a particular polar angle, the condition is \(\partial p^{(\theta)}/\partial \theta = 0\); if the rigid surface is specified at a particular azimuthal angle, the condition is \(\partial p^{(\psi)}/\partial \psi = 0\).
☸ For a boundary condition on a Cartesian coordinate, show that the particle velocity attains an extremum at a pressure-release surface. Also show that the particle velocity is zero at a rigid surface. For a boundary condition on a spherical coordinate, does the particle velocity attain an extremum at a pressure-release surface? Is the particle velocity zero at a rigid surface? [answer]

Boundary condition on Cartesian coordinate. The boundary condition at a pressure-release surface is that \(p= 0\). Therefore, when the continuity equation \(\gradient \cdot (\rho \vec{u}) + \partial \rho/\partial t = 0\) is linearized and applied to a time-harmonic pressure, one obtains the condition \begin{align}\tag{i}\label{contersslkfsdlkjf} j\omega p + \rho_0 c_0^2 \gradient\cdot \vec{u} = 0, \end{align} where the linear relation \(\rho' c_0^2= p\) has been used to eliminate density. In Cartesian coordinates, equation (\ref{contersslkfsdlkjf}) applied at the \(n\)th surface reads \[j\omega p + \rho_0 c_0^2 \frac{\partial u^{(n)}}{\partial n} = 0,\] from which it can be seen that at the pressure release surface, \(\frac{\partial u^{(n)}}{\partial n} = 0\), i.e., the particle velocity is extremized.

Meanwhile the boundary condition at the \(n\)th rigid surface is that \(\partial p/\partial n = 0\). Therefore, by the the linearized momentum equation for a time-harmonic particle velocity, \begin{align}\tag{i}\label{sdkjjlsdflkjafsamsdfm} \gradientp + j\omega \rho_0 \vec{u} &= 0\,, \end{align} from which it can be see that at the rigid surface defined along coordinate \(n\), \(u^{(n)} = 0\), i.e., the particle velocity vanishes.

Boundary condition on a spherical coordinate. The story is different for a boundary condition on a spherical coordinate. For example, at a pressure release surface defined at a particular radius, equation (\ref{contersslkfsdlkjf}) reads \[j\omega p + \rho_0 c_0^2 \bigg[u^{(r)}_r + \frac{2}{r}u^{(r)} \bigg] = 0,\] from which it can be seen that the radial component of the particle velocity does not go to zero when \(p=0\) (Only in the limit \(r\to \infty\) does the particle velocity go to \(0\)). This is a distinction between Cartesian boundary conditions and spherical boundary conditions.

However, for rigid surfaces defined along a spherical coordinate, equation (\ref{sdkjjlsdflkjafsamsdfm}) guarantees that the particle velocity vanishes at the boundary.
☸ Do Blackstock problem 10-13 two different ways, first in the "conventional" orientation with spherical coordinates defined as the original figure is drawn, and second in a \(90^\circ\)-rotated coordinate system in which the flat part of the hemisphere is in the plane defined by \(\psi = 0\) and \(\psi = \pi\). [answer]

See here for the solution. Note that Blackstock's associated Legendre functions \(P^1_1, P^1_2, P^1_3\), and \(P^3_3\) on page 348 follow a different convention than what is listed on Wikipedia, Wolfram, and most other references. These polynomials (and in general, those with odd \(m\), are off by a factor of \(-1\) from the "normal" convention).
What is the degeneracy of modes in a spherical enclosure? Bonus: how does this compare to the degeneracy in the hydrogen atom? Careful! I am using Blackstock's convention in which \(l\), the orbital angular momentum number of quantum mechanics, is interchanged with \(m\). [answer]

Note that the eigenfrequencies are independent of \(m\). They only depend on \(n\) (the principal quantum number, if you will) and \(l\), the index of the root of the Bessel function. Therefore, all the eigenfunctions with the same \(n\) and \(l\) indices but different values of \(m\) correspond to the same eigenfrequency. Recall that \(n = 0,1,2,\dots\) and \(m = 0, 1, 2, \dots n\). There are \(n+1\) values of \(m\) for every \(n\). The degeneracy is therefore \(n +1\). (If negative values of \(m\) were included, the degeneracy would be \(2m + 1\)).

In the hydrogen atom, the degeneracy is \(n^2\), and if spin is included, \(2n^2\).

For more on parallels between acoustics and quantum mechanics related to spherical coordinates, see these notes.
Solve the wave equation for the air trapped between two concentric pressure-release spheres, where the inner radius is \(a\) and the outer radius is \(b\). Numerically obtain the eigenfrequencies. [answer]

This is Blackstock's problem 10-10 of Fundamentals of Physical Acoustics, so I cannot post the full solution, but displayed here are numerically determined combinations of \(ka\) and \(kb\) that correspond to the eigenfrequencies for sound enclosed between two concentric pressure-release spheres. Bright spots on the surface plots correspond to eigenfrequencies.
Solve the wave equation in an axisymmetric spherical enclosure of radius \(a\) and angular distribution \(f(\theta)\), such that the field at \(r=a\) is \(p(a,\theta,t) = p_0 f(\theta) e^{j\omega t}\). [answer]

See here for the solution.
☸ Why do eigenfrequencies of sound spherical coordinates not depend on the azimuthal index \(m\)? How do the eigenfrequencies of acoustic wave equation relate to the eigenfrequencies of the quantum mechanical equation? Note: the letters conventionally used for the indices corresponding to spherical harmonics in acoustics are flipped from those used in quantum mechanics! [answer]

See here for a discussion. Thanks to J. S. Hallveld for his insights.
Attention is now turned to radiation problems. What limit on the dimensionless parameter \(kr\) of spherical radiation corresponds to far field radiation? What limit corresponds to near field radiation? [answer]

\(kr \gg 1\) corresponds to far-field radiation, and \(kr \ll 1\) corresponds to near-field radiation.
What does the combination of limits \(kr \gg 1\) and \(ka \ll 1\) correspond to physically? What kind of directivity does this limit reduce to? [answer]

This is the subwavelength limit of the far field. The radiation is governed purely by diffraction and is in the form of a monopole, which is proportional to the volume velocity \(Q_0\). The directivity of a monopole is \(1\).
And what does the combination of limits \(kr \gg 1\) and \(ka \gg 1\) correspond to? What kind of directivity does this limit reduce to? Bonus: How do these limits relate to the structure of the cosmic microwave background radiation, and hence the distribution of galaxies in the universe today? [answer]

This is the geometric acoustics limit of the far field. The radiation is non-diffractive, and is simply a projection of the original source condition of rays to \(r = \infty\).

The early universe was a plasma in which there existed an outward pressure due to photon-matter interactions, as well as an inward force due to gravity. This balance of attractive and repulsive force created a harmonic potential, giving rise to acoustic waves. The acoustic waves were spherical traveling waves propagating outward over vast distances. Thus the far field limit \(kr\gg 1\) appropriately describes these spherical waves (i.e., The propagation distance was much greater than the wavelength). Further, the sources of sound were much larger than a wavelength, i.e., \(ka \gg 1\), and thus the structure of the initial conditions was projected into the far field. When the universe cooled sufficiently such that the protons and neutrons combined to form hydrogen atoms, these atoms were arranged in the structure of the far-field geometric acoustic limit of the spherical acoustic oscillations. This so-called recombination (the formation of hydrogen) released photons that have redshifted (due to the expansion of the universe) into the microwave spectrum: this is the cosmic microwave background radiation. This initial distribution of matter, preserved as microwave radiation, explains the structure of the universe today, with denser regions giving rise to galaxies. See this video for a nice animation of these oscillations.

Note that before recombination, photons could not travel freely; thus acoustic waves could propagate while electromagnetic waves could not. The old joke that sound came before light because "God said, 'Let there be light'" is actually true!
Obtain the field radiated by a general axisymmetric spherical velocity source of radius \(a\). Suppose the field at \(r=a\) has the form \(u_r (a,\theta,t) = u_0 f(\theta) e^{j\omega t}\). Take the limit \(kr \to \infty\). Then further apply the limits \(ka \ll 1\) and \(ka \gg 1\). [answer]

See here for the solution.
Solve the spherical radiation problem for the boundary conditions \begin{align*} u^{(r)}(a,\theta,t) &= \begin{cases} u_0e^{j\omega t}, \quad \text{ for } \theta \in [0,\pi/2)\\ -u_0e^{j\omega t}, \quad \text{ for } \theta\in [\pi/2, \pi]\,, \end{cases} \end{align*} i.e., the bipolar pulsating sphere. Once the solution is obtained, take the limit as \(kr\gg 1\) and \(ka\ll 1\). It will be helpful to note that \(h_n^{(2)}(kr) \to e^{j(\omega t - kr)}/r\) as \(kr \to \infty\), and that \(1/h_n'(ka) \to j(ka)^3/2\) as \(ka \to 0\). Also note that in this limit, the leading term corresponds to \(n=1\) (because the \(n=0\) term is \(0\)). [answer]

Noting that the solution must be time harmonic, suppress the linear combination \begin{align*} \begin{Bmatrix} e^{j\omega t}\\e^{-j\omega t} \end{Bmatrix} \end{align*} i.e., solve the Helmholtz equation. Note that there is no dependence on \(\psi\), the azimuthal angle. Therefore \(m=0\). Also, the Hankel functions of the first kind are tossed since waves are outgoing. Let \(h^{(2)}_n \equiv h_n\). Then general solution reads \begin{align}\label{sldkfjsdlkfjalsdfjmdkl} p(r,\theta) = \sum_{n=0}^{\infty} A_n h_n{(kr)} P_n(\cos\theta) \,.\tag{i} \end{align} To satisfy the velocity boundary conditions, the linearized momentum equation must be invoked for a time harmonic velocity: \begin{align*} u^{(r)} &= -\frac{1}{j\omega \rho_0}\frac{\partial p}{\partial r}\\ &= -\frac{A_nk}{j\omega \rho_0} h_n'(kr) P_n(\cos\theta)\\ &=-\frac{1}{j\rho_0c_0} h_n'(kr)P_n(\cos\theta) \end{align*} Therefore, at \(r=a\), \begin{align*} -\frac{A_n}{j\rho_0c_0} h_n'(ka)P_n(\cos\theta) &= \begin{cases} u_0, \quad \text{ for } \theta \in [0,\pi/2)\\ -u_0, \quad \text{ for } \theta \in [\pi/2, \pi]\\ \end{cases} \end{align*} Thus \begin{align*} A_nP_n(\cos\theta) &= -\frac{j\rho_0c_0}{h_n'(ka)} \begin{cases} u_0, \quad \text{ for } \theta \in [0,\pi/2)\\ -u_0, \quad \text{ for } \theta \in [\pi/2, \pi]\\ \end{cases} \end{align*} To solve for the expansion coefficients \(A_n\), multiply both sides by \(P_m(\cos\theta)\sin\theta d\theta\) and integrate: \begin{align*} \int_{0}^{\pi} A_nP_n(\cos\theta)P_m(\cos\theta)\sin\theta d\theta &= -\frac{j\rho_0c_0 u_0}{h_n'(ka)} \bigg[ \int_{0}^{\pi/2} P_m(\cos\theta) \sin\theta d\theta - \int_{\pi/2}^{\pi} P_m(\cos\theta)\sin\theta d\theta \bigg]\\ A_n \frac{2}{2n+1}&= \frac{j\rho_0c_0 u_0}{h_n'(ka)} \bigg[ \int_{0}^{1} P_n(z) dz - \int_{-1}^{0} P_n(z) dz\bigg] \end{align*} \(P_n(z) = P_n(-z)\) is for even \(n\), so the term in the square brackets is \(0\) in that case. Meanwhile, \(P_n(-z) = -P_n(z)\) for odd \(n\), so \begin{align}\label{sldkfjsdlkafjlsdk} A_n &= (2n+1)\frac{j\rho_0c_0 u_0}{h_n'(ka)} \int_{0}^{1} P_n(z) dz \tag{ii} \end{align} To evaluate the integral, use the property \((2n+1)P_n(z) = P_{n+1}'(z) - P_{n-1}'(z)\), which is integrated trivially using the fundamental theorem of calculus: \begin{align*} \int_{0}^{1}P_n(z)dz &= \frac{1}{2n+1} \int_{0}^{1} \big[P_{n+1}'(z) - P_{n-1}'(z)\big]dz\\ &= \frac{1}{2n+1}[P_{n+1}(1) - P_{n-1}(1) - P_{n+1}(0) + P_{n-1}(0)]\,. \end{align*} Since the Legendre polynomials are normalized such that \(P_n(1) = 1\), the first two terms above cancel, giving \begin{align*} \int_{0}^{1}P_n(z)dz &= \frac{1}{2n+1} [- P_{n+1}(0) + P_{n-1}(0)]. \end{align*} The two Legendre polynomials above can be combined into one by noting that \((2n+1)zP_n(z) = (n+1)P_{n+1}(z) + nP_{n-1}(z)\), or for \(z=0\), \[-P_{n+1}(0) = \frac{n}{n+1}P_{n-1}(0)\] Thus the integral becomes \begin{align*} \int_{0}^{1}P_n(z)dz &= \frac{1}{2n+1}\bigg[\frac{2n+1}{n+1} P_{n-1}(0)\bigg] = (n+1)^{-1}P_{n-1}(0)\,. \end{align*} and equation (\ref{sldkfjsdlkafjlsdk}) becomes \begin{align*} A_n &= \frac{2n+1}{n+1}\frac{j\rho_0c_0 u_0}{h_n'(ka)}P_{n-1}(0) \end{align*} The problem is solved by inserting the coefficients above into equation (\ref{sldkfjsdlkfjalsdfjmdkl}): \begin{align}\tag{iii}\label{lksjdaflkj} p(r,\theta) = j\rho_0c_0 u_0 \sum_{n=0}^{\infty} \frac{2n+1}{n+1}\frac{h_n{(kr)}}{h_n'(ka)}P_{n-1}(0) P_n(\cos\theta) \end{align}

Taking the limits of equation (\ref{lksjdaflkj}) for \(n =1\) (the leading order term) gives \[p = -\frac{3}{4} \rho_0c_0 u_0 (ka)^3 \frac{e^{j(\omega t - kr)}}{r} \cos\theta\,,\] i.e., the dipole directivity pattern.
Write the pressure field due to a pair of antiphase monopole separated by distance \(2 h\) in the far field limit, \(r\gg h\). [answer]

See here for the solution.
Calculate the pressure field due to a translating sphere, for which the boundary condition is \[u^{(r)}(r= a) = u_0 e^{j\omega t} \cos\theta.\] Note that \(h_1(kr) = e^{-jkr}(1+1/jkr)/ kr\). Evaluate the pressure field in the subwavelength limit, noting that \(h_1'(ka) \to 2/jka^3\) for \(ka \ll 1\). Identify the directivity in this limit. [answer]

See here for the solution. Writing \(h_1(kr) = e^{-jkr}(1+1/jkr)/ kr\) and evaluating the solution in the limit that \(ka \ll 1\), the solution becomes \[p = \frac{1}{2} k^2 a^3\rho_0 c_0 u_0 \cos \theta (1+ 1/jkr) e^{j(\omega t - kr)}/r\,.\] The directivity in this limit is that of a dipole: \(\cos\theta\).
An acoustic monopole is a ________ ________ source, while an acoustic dipole is a ________ source. [answer]

volume velocity (or mass); force. Note that the force exerted by the dipole is proportional to the so-called "entrained mass" of the fluid.
Create a dipole by positioning two out-of-phase monopoles a distance \(2h\) apart along the line \(\theta = 0\). Take the \(r\gg h\) limit and thus derive the dipole directivity pattern. [answer]

The sum of the monopoles is given (exactly) by \begin{align*} p = \frac{A}{r_1} e^{j(\omega t - kr_1)} -\frac{A}{r_2} e^{j(\omega t - kr_2)}\,. \end{align*} In the far field, the denominators of the amplitudes are approximated \(r\), and the phases are approximated by \(r_1 \simeq r - h\cos\theta\) and \(r_2 \simeq r + h\cos\theta\). This leads to \begin{align}\label{slkdfjsdlkfjsldkfaj}\tag*{pair of monopoles} p = \frac{2Aj}{r} e^{j(\omega t - kr)}\sin (kh \cos\theta)\,. \end{align} We know that this result is in the far field because the angular and radial dependence is separated. Now letting \(kh \ll 1\), the pressure approaches that of a point dipole: \begin{align*} p = \frac{2Aj}{r} kh \cos\theta e^{j(\omega t - kr)} \,. \end{align*}
Calculate the power \(W\) radiated by a pair of out-of-phase monopoles. Using the expression for the \ref{slkdfjsdlkfjsldkfaj} derived in the previous problem, note that \(p/p_\text{free} = 2j\sin (kh \cos\theta)\), since \(p_\text{free} = A e^{j(\omega t - kr)}/r\). [answer]

The power is given by the surface integral of the intensity. The intensity is calculated by noting that \(\langle I \rangle/\langle I_\text{free}\rangle = |p/p_\text{free}|^2 = 4\sin^2(kh\cos\theta)\). Thus \(\langle I\rangle = \langle I_\text{free}\rangle 4\sin^2(kh\cos\theta)\). \begin{align*} W&= 4 \langle I_\text{free} \rangle \, \oint \sin^2 (kh \cos\theta) \vec{e}_r \cdot d\vec{A}\\ &= 4 \langle I_\text{free} \rangle \,\int_0^{\pi/2} \int_{0}^{2\pi} \sin^2 (kh \cos\theta)r^2\sin\theta d\theta d\psi\\ &= 8 \langle I_\text{free} \rangle \,\pi r^2 \int_{0}^{\pi/2} \sin^2 (kh \cos\theta) \sin\theta d\theta \end{align*} The integral above is taken by letting \(q = \cos\theta\). The result is \[W = 4\,\pi r^2 I_\text{free} [1 - \sin(2kh)/2kh]\,.\] Note that \(4\,\pi r^2 \langle I_\text{free}\rangle = W_\text{free}\), the power radiated by a monopole, so the above result can be written as \[W = W_\text{free} [1 - \sin(2kh)/2kh]\,.\] Note that Blackstock does not use the \(\langle \dots \rangle\) notation to denote "time avarerage of \(\dots\)." Blackstock's "\(I\)" corresponds to \(\langle I \rangle\) on this site.
Create a longitudinal quadrupole by positioning two out-of-phase dipoles along the line \(\theta = 0\), separated by distance \(h\). Recall that the pressure field due to each dipole is given by the equation for the \ref{slkdfjsdlkfjsldkfaj}. Take the \(kh \gg 1\) limit to obtain the directivity of a point quadrupole. [answer]

The pressure field is given by \begin{align*} p = p_d\big[ e^{jkh\cos(\theta)/2} - e^{-jkh\cos(\theta)/2}\big] \end{align*} where \begin{align*} p_d = \frac{2Aj}{r} kh \cos\theta e^{j(\omega t - kr)} \,. \end{align*} Putting the equations together gives \begin{align}\label{sldkfdssdfsdfasdlf}\tag{i} p = \frac{2Aj}{r} kh \cos\theta e^{j(\omega t - kr)} \sin [kh\cos(\theta)/2] \end{align} Taking the \(kh \ll 1\) limit of equation (\ref{sldkfdssdfsdfasdlf}) gives the directivity a point quadrupole: \[p = \frac{Aj}{r} (kh)^2 \cos^2\theta\, e^{j(\omega t - kr)}\,.\]

Chapter 11: Cylindrical waves

Obtain the general solution to the wave equation in cylindrical coordinates. [answer]

See here for a video solution of the wave equation in cylindrical coordinates.
☸ In spherical solutions to the wave equation, what are the names of the three indices used? What do they correspond to physically? What possible values can the indices equal? In cylindrical coordinates, what indices are used, what do they correspond to physically, and what are their possible values? Comment on the similarities and differences. [answer]

Note that Blackstock's convention is used in the following discussion.

In spherical coordinates, \(n = 0,1,2,\dots\) corresponds to the order of the spherical Bessel function. \(n\) also appears as the index of the Legendre polynomial and the lower index of the associated Legendre function. Meanwhile, \(l = 1,2,3,\dots\) corresponds to the zero of the spherical Bessel function. Finally, \(m = 0, 1,2,\dots, n\) appears in the harmonic azimuthal dependence, as well as in the top index of the associated Legendre polynomial. The eigenfrequencies in spherical coordinates depend only on \(n\) and \(l\) in even the most general case.

In cylindrical coordinates, \(m = 0,1,2,\dots\) is the order of the Bessel function, while \(n = 1,2,3,\dots\) corresponds to the zero of the Bessel function. \(m\) is also the index corresponding to the harmonic polar dependence. \(l = 1,2,3,\dots\) (and sometimes \(0\)) is the index corresponding to the \(z\)-dependence. The eigenfrequencies in cylindrical coordinates depend on all three indices in the most general case.

One similarity between spherical and cylindrical solutions is that the Bessel functions and polar functions in either case share the same index. In spherical coordinates, that index is \(n\); in cylindrical coordinates, that index is \(m\). In light of this, I wish Dr. Blackstock had used \(n\) instead of \(m\) for the index in cylindrical coordinates, to preserve this similarity with spherical coordinates.

One difference between spherical and cylindrical solutions is that \(n\) in spherical coordinates is necessarily an integer, but \(m\) in cylindrical coordinates can taken on non-integer (and in fact irrational) values. This happens in cylindrical wedge problems. In this case, the Latin \(m\) is replaced with the Greek \(\mu\).

One should not be militant about the names of indices; it is much more important to have the form of solution correct. In summary, the general solution in spherical coordinates is given by \begin{align*} R(r)\Theta(\theta)\Psi(\psi)= \begin{Bmatrix}j_n(k_{nl}r) \\n_n(k_{nl}r)\end{Bmatrix} \begin{Bmatrix}P^m_n(\cos\theta) \\ Q^m_n(\cos\theta)\end{Bmatrix} \begin{Bmatrix}\cos m\psi \\ \sin m\psi \end{Bmatrix}\begin{Bmatrix}\cos \omega t \\ \sin \omega t\end{Bmatrix} \end{align*} while that in cylindrical coordinates is given by \begin{align*} R(r)\Theta(\theta)Z(z)= \begin{Bmatrix}J_m(k_{mn}r) \\N_m(k_{mn}r)\end{Bmatrix} \begin{Bmatrix}\cos m\theta \\ \sin m\theta\end{Bmatrix} \begin{Bmatrix}\cos lz \\ \sin lz\end{Bmatrix}\begin{Bmatrix}\cos \omega t \\ \sin \omega t\end{Bmatrix} \end{align*}
Obtain the complete solution to the 2D wave equation for a circular drumhead that is clamped at radius \(r =a\) and that is struck at \(r=0\) at \(t=0\). Let \(\eta\) be the displacement of the drumhead. The initial conditions are that the drumhead is initially silent, \(\eta = 0\), and the initial velocity is \(\dot{\eta} = v_0 \delta(r)/2\pi r\). [answer]

Start with the general solution to the wave equation in \(r\) and \(\theta\). Neglect the Neumann functions since the origin is included. \begin{align*} \eta(r,\theta,t) = J_m(kr) \begin{Bmatrix}\cos m\theta \\ \sin m\theta\end{Bmatrix} \begin{Bmatrix}\cos \omega t \\ \sin\omega t\end{Bmatrix} \end{align*} Applying the radial boundary condition gives the eigenfrequencies: \begin{align*} J_m(ka) = 0\quad \implies\quad k_{mn} = \frac{\alpha_{mn}}{a}\quad \implies\quad f_{mn} = \frac{c_0\alpha_{mn}}{2\pi a}\,, \end{align*} where \(\alpha_{mn}\) is the \(n\)th root of the Bessel function of order \(m\). The angular dependence can be written more conveniently as \(\cos(m\theta + \psi_m)\). Thus the general solution becomes \begin{align*} \eta(r,\theta,t) = \sum_{n=1}^\infty \sum_{m=0}^\infty J_m(\alpha_{mn}'r/a) \cos (m\theta +\psi_m)(C_{mn}\cos \omega_{mn} t + D_{mn}\sin\omega_{mn} t) \end{align*} The condition that the drumhead is initially silent implies that \(C_{mn} = 0\). Also, since the initial condition is independent of \(\theta\), \(m=0\): \begin{align}\tag{i}\label{sldkfjasdlfj} \eta(r,\theta,t) = \sum_{n=1}^\infty D_{n} J_0(\alpha_{0n}r/a) \sin\omega_{n} t \end{align} To determine \(D_{n}\), the initial conditions \(\eta = 0\) and \(\dot{\eta} = v_0 \delta(r)/2\pi r\) at \(t=0\) are utilized. Thus, \begin{align*} \dot{\eta} = \frac{v_0 \delta(r)}{2\pi r} = \sum_{n=1}^\infty D_{n} \omega_{n} J_0(\alpha_{0n}r/a) \end{align*} Multiplying both sides by \(J_0(\alpha_{0n'} r/a)r dr\) and integrating from \(r=0\) to \(r=a\) gives \begin{align}\tag{ii}\label{lskdfjalskdfj} \frac{v_0}{2\pi}\int_{0}^{a} \delta(r) J_0(\alpha_{0n'} r/a) dr &= \sum_{n=1}^\infty \omega_{n} D_{n} \int_{0}^{a} J_0(\alpha_{0n'}r/a) J_0(\alpha_{0n}r/a)r dr \end{align} The integral on the left-hand side is trivial by the sifting property of the delta function. \[\frac{v_0}{2\pi}\int_{0}^{a} \delta(r) J_0(\alpha_{0n'} r/a) dr = \frac{v_0}{2\pi} J_0(0) = \frac{v_0}{2\pi} \] The right-hand side of equation (\ref{lskdfjalskdfj}) is the orthogonality relation for the order 0 Bessel function. Making the substitution \(x \equiv r/a\) makes this more clear: \begin{align*} \int_{0}^{a} J_0(\alpha_{0n'}r/a) J_0(\alpha_{0n}r/a)r dr &= a^2\int_{0}^{1} J_0(\alpha_{0n'}x) J_0(\alpha_{0n}x)x dx\\ &= \frac{a^2}{2} [J_0'(\alpha_{0n'})]^2\delta_{nn'} \end{align*} Thus equation (\ref{lskdfjalskdfj}) becomes \begin{align*} \frac{v_0}{2\pi} &= \frac{a^2}{2} \sum_{n=1}^\infty \omega_{n} D_{n} [J_0'(\alpha_{0n'})]^2\delta_{nn'} \end{align*} Solving for \(D_n\) gives \[ D_{n} =\frac{v_0}{[J_0'(\alpha_{0n})]^2 \omega_{n} \pi a^2}.\] The complete solution is found by substituting the above into equation (\ref{sldkfjasdlfj}): \begin{align*} \eta(r,\theta,t) = \frac{v_0}{\pi a^2}\sum_{n=1}^\infty \frac{J_0(\alpha_{0n}r/a)}{[J_0'(\alpha_{0n})]^2 \omega_{n} } \sin\omega_{n} t \end{align*}
A driven circular drumhead obeys the inhomogeneous wave equation \[\nabla^2 \eta - \frac{1}{c^2}\eta_{tt} = -\frac{p_s}{\mathcal{T}_l},\] where \(p_s\) is the drive function, considered here to be \(p_s = p_{0} e^{j\omega t}\). Describe a situation in which this be the drive function of the drumhead. Solve the inhomogeneous wave equation. [answer]

A common situation in which this rather simplistic function would drive a drumhead is a bass guitar driving the drumhead of a snare drum. The low E-string of a bass guitar produces low-frequency sound of a wavelength 8.5 meters. Meanwhile, the snare drum's diameter is about 0.3 meters. Thus there are two orders of magnitude that separate the length scale of the drive frequency and the snare drum's diameter. In this case, the drive frequency acts on the the snare drum as simply a function of time, not space.

To solve the inhomogeneous wave equation, first note that the time dependence will be \(e^{j\omega t}\) (that of the drive frequency), and that the only spatial dependence will be radial, i.e., \(\eta(r,t) = R(r) e^{j\omega t}\). Thus the inhomogeneous PDE to solved reduces to an inhomogeneous ODE: \begin{align*} R'' + \frac{1}{r}R' + k^2 R = -\frac{p_0}{\mathcal{T}}. \end{align*} The solution to this ODE is the sum of the homogeneous and inhomogeneous parts. The homogeneous solution is the solution to Bessel's equation of order \(0\): \(A \,J_0(kr)\). For the inhomogeneous solution, it is noted that the right-hand side is constant, so a trial solution \(C\) is used giving \(C = -p_0/k^2\mathcal{T}\). Thus the solution to the ODE is \begin{align*} R(r) = A \,J_0(kr) -\frac{p_0}{k^2\mathcal{T}}\,. \end{align*} Applying the boundary condition that \(R= 0\) at \(r=a\) gives \begin{align*} A= \frac{p_0}{k^2\mathcal{T}J_0(ka)} \end{align*} The solution is thus \begin{align*} \eta (r,t) &= \frac{p_0}{k^2\mathcal{T}}\bigg[\frac{J_0(kr)}{J_0(ka)} - 1\bigg] e^{j\omega t} \end{align*} Note that when \(ka = \alpha_{0n}\), the response goes to \(\infty\).
Part 1. Solve the 2D wave equation in \(\eta(r,\theta)\) for a pie-shaped drumhead subtending \(45^\circ\), where one edge, say \( \theta = 0\), is free, while the curved boundary at \(r = a\) and the other edge at \(\theta = 45^\circ\) are clamped: Find the eigenfrequencies and identify the lowest one. Part 2. Suppose there is an initial displacement on the membrane of \(\eta_0\), which would correspond to a "plucked" initial condition. Also assume there is no initial velocity: \begin{align*} \eta(r,\theta,0) &= \begin{cases} \eta_0,\quad &\theta = [0,\,\pi/4),\, r = [0,a]\\ 0,\quad &\theta = [\pi/4,\, 2\pi) \end{cases}\\ \dot{\eta}(r,\theta,0) &= 0 \end{align*} Apply the initial condition to the eigenfunctions found in part 1 to find \(C_{mn}\) and \(D_{mn}\). Leave the relevant expansion coefficients in integral form, and evaluate the integral for \(m=0\) only. Compare the coefficients for \(m=0\) to Blackstock's equation (11.B-13) on page 400 for a circular drumhead clamped at \(r=a\) subject to the analogous "plucked'' initial condition. [answer]

See here for the solution.
What is the general solution to the 3D wave equation for sound in a hollow cylinder of length \(L\) and radius \(a\) with rigid walls? Which eigenfrequencies recover those corresponding purely harmonic axial modes (no propagation in \(r\) and \(\theta\))? Which eigenfrequencies correspond to purely radial modes (no dependence in \(\theta\) and \(z\))? Is it possible to have pure spinning modes? [answer]

See here for the solution. Setting \(m = 0\) and \(n = 1\) results in purely axial modes because \(\alpha'_{01}= 0\), and thus the radial dependence is eliminated \(J_0(0)=1\). Setting \(m = 0\) and \(l =0\) gives purely radial modes because the angular dependence and axial dependence are both eliminated in that case.

It is not possible to have pure spinning modes. One way to rationalize this is to note that there is no "angular wavenumber." One can also see by inspection that there must exist radial modes if there exist angular modes, because both depend on the same index \(m\).
Solve the wave equation for sound in between two concentric cylinders of length \(L\), inner radius \(a\), and outer radius \(b\). Let all boundaries be pressure-release. Do not attempt to find the eigenfrequencies explicitly. [answer]

See here for the solution.
Calculate the pressure field due to a uniformly pulsating cylinder, for which the velocity boundary condition is \(u^{(r)}(r=a) = u_0 e^{j\omega t}\). What makes the near field of the impedance of the uniformly pulsating cylinder interesting? [answer]

See here for the solution. The near field impedance can be calculated given the \(kr \ll 1\) limit of the Hankel function. What makes it interesting is that it depends on \(c_0\). In contrast, the near field spherical impedance relation is independent of \(c_0\).
Calculate the pressure field due to a translating cylinder, for which the velocity boundary condition is \(u^{(r)}(r=a) = u_0 \cos\theta \, e^{j\omega t}\). [answer]

See here for the solution.
Consider a waveguide with pressure-release surfaces at \(z = 0\) and \(z = D\). A vertically oriented cylindrical source of radius \(a\) extending from \(z = 0\) to \(z = D\) pulses radially, i.e., \(u(a,\theta,z,t) = u_0 e^{j\omega t}\). Solve the pressure wave equation for this configuration [answer]

Here is the solution for (1) a radially pulsating cylindrical source of sound extending between two pressure-release parallel planes. Prof. Blackstock mentions this kind of waveguide on page 432 in Fundamentals of Physical Acoustics. He solves for (2) a radially pulsating cylindrical source between two rigid, parallel planes on page 430, and assigns the case of (3) a radially pulsating cylindrical source between one rigid boundary and one pressure-release boundary (a 0th-order model of sound in the ocean) as problem 12-13. Interestingly, case (1) and (3) excite many modes, but case (2) excites only the lowest mode.

Chapter 12: Waveguides

Find the eigenmodes, cutoff frequency, phase speed, and group speed for an infinite rectangular duct of length \(a\) and height \(b\), where \(\partial p/\partial x = 0\) from \(x \in [0,a]\) and \(\partial p/\partial y = 0\) from \(y \in [0,b]\). For what drive frequencies \(\omega\) does the sound propagate? Why does the drive frequency \(\omega\) not bear the indices of the modes? [answer]

The general solution is \begin{align*} p(x,y,z,t) = \begin{Bmatrix} \cos k_xx \\ \sin k_xx \end{Bmatrix} \begin{Bmatrix} \cos k_yy \\ \sin k_yy \end{Bmatrix} e^{j(\omega t -k_zz)}\,. \end{align*} where the relationship between wavenumbers is \begin{align*} k_z = \sqrt{k^2 - k_x^2 - k_y^2}\,. \end{align*} Applying the boundary conditions at \(x =0\) and \(y=0\) eliminates the \(\sin k_xx\) and \(\sin k_yy\) terms, and applying the boundary conditions at \(x = a\) and \(y=b\) gives \begin{alignat*}{2} \sin k_x a &= 0 \quad &&\implies\quad k_x = \frac{m\pi}{a}\\ \sin k_y b &= 0 \quad &&\implies\quad k_y = \frac{n\pi}{b} \end{alignat*} Thus the projection of the wavenumber in the \(z\)-direction is \begin{align}\tag{i}\label{beasdfsd} \beta_{mn} = \sqrt{(\omega/c_0)^2 - (m\pi/a)^2 - (n\pi/b)^2}\,. \end{align} \(\omega\) above does not bear the modal indices \(m\) and \(n\) because it is the frequency at which the system is driven. In other words, \(\omega\) is not an eigenfrequency. The cutoff frequency, however, does bear the indices \(m\) and \(n\) because it is depends purely on the system, i.e., it is independent of the nature of the excitation. The cutoff frequency is the frequency below which \(\beta_{mn}\) is evanescent. It is found by setting the radicand (''the thing under the square root'') equal to 0 and solving for \(\omega^{(c)}\): \begin{align*} 0&= {[\omega^{(c)}/c_0]^2 - (m\pi/a)^2 - (n\pi/b)^2}\\ \omega^{(c)}_{mn} &= c_0 \sqrt{(m\pi/a)^2 + (n\pi/b)^2}\\ f^{(c)}_{mn} &= \frac{c_0}{2} \sqrt{(m/a)^2 + (n/b)^2}\,. \end{align*} Thus, since \([\omega^{(c)}_{mn}]^2/c_0^2 = (m\pi/a)^2 + (n\pi/b)^2\), equation (\ref{beasdfsd}) can be written as \begin{align*} \beta_{mn} &= \frac{1}{c_0}\sqrt{\omega^2 - [\omega^{(c)}_{mn}]^2}\\ &= \frac{\omega}{c_0}\sqrt{1 - [\omega^{(c)}_{mn}/\omega]^2} \end{align*} From the expression above, it can be seen that \(\beta_{mn}\) is real and positive if the drive frequency \(\omega\) is greater than the cutoff frequency \(\omega^{(c)}_{mn}\), i.e., the \(m\, n^\text{th}\) mode cannot propagate below the \(m\, n^\text{th}\) cutoff frequency.

Meanwhile, the phase speed is \(c_\text{ph} = \omega/k_z = \omega/\beta_{mn}\): \begin{align*} c_\text{ph} = \frac{c_0 }{\sqrt{1 - [\omega^{(c)}_{mn}/\omega]^2}}\,. \end{align*} The group speed is \(c_\text{gr} = {d\omega}/{d\beta_{mn}}\): \begin{align*} c_\text{gr} &= \bigg[\frac{d\beta_{mn}}{d\omega}\bigg]^{-1} \\ &= \bigg[\frac{1}{c_0 \sqrt{1-(\omega^{c}_{mn}/\omega)^2}}\bigg]^{-1}\\ &= c_0 \sqrt{1-(\omega^{c}_{mn}/\omega)^2} \end{align*}
Find the eigenmodes, cutoff frequency, phase speed, and group speed for an infinite cylindrical duct of radius \(a\), where \(\partial p/\partial r = 0\) at \(r=a\). For what drive frequencies \(\omega\) does the sound propagate? Why does the drive frequency \(\omega\) not bear the indices of the modes? [answer]

The general solution is \begin{align*} p(r,\theta,z,t) = J_m(k_rr) \begin{Bmatrix} \cos m\theta\\\sin m\theta \end{Bmatrix} e^{j(\omega t -k_zz)}\,. \end{align*} where the relationship between wavenumbers is \begin{align*} k_z = \sqrt{k^2 - k_r^2}\,. \end{align*} Applying the boundary condition at \(x =a\) gives \begin{align*} J'_m(k_ra) = 0 \quad \implies \quad k_r = \frac{\alpha'_{mn}}{a} \end{align*} Thus the projection of the wavenumber in the \(z\)-direction is \begin{align}\tag{i}\label{betassldfkjl} \beta_{mn} = \sqrt{(\omega/c_0)^2 - ({\alpha'_{mn}}/{a})^2}\,. \end{align} The cutoff frequency is found by setting \begin{align*} 0&= {[\omega^{(c)}/c_0]^2 - ({\alpha'_{mn}}/{a})^2}\\ \omega^{(c)}_{mn} &= c_0 {\alpha'_{mn}}/{a}\\ f^{(c)}_{mn} &= c_0 {\alpha'_{mn}}/{2\pi a}\,. \end{align*} Thus, equation (\ref{betassldfkjl}) can be written as \begin{align*} \beta_{mn} &= \frac{1}{c_0}\sqrt{\omega^2 - [\omega^{(c)}_{mn}]^2}\\ &= \frac{\omega}{c_0}\sqrt{1 - [\omega^{(c)}_{mn}/\omega]^2} \end{align*} As is the case for the rectangular duct, the \(m\, n^\text{th}\) mode cannot propagate below the \(m\, n^\text{th}\) cutoff frequency.

The phase and group speeds have the same functional form as for the rectangular waveguide; the expression for the cutoff frequency is the only difference.
☸ Calculate the pressure field due to a baffled circular piston of radius \(b\) positioned with its center on the axis of a cylindrical tube of radius \(a\). The boundary conditions at \(z=0\) are \begin{alignat*}{2} u_z &= u_0 e^{j\omega t},\quad &&r\in [0,b]\\ u_z &= 0,\quad &&r\in (b,a] \end{alignat*} and \(\partial p/\partial r = 0\) at \(r=a\) for all \(z\). Note that \[\int_0^1 J_m(\alpha'_{mn} x )J_m(\alpha'_{mn'} x) \,x\, dx = \frac{1}{2}[1-(m/\alpha'_{mn})^2] J^2_m(\alpha'_{mn'}) \delta_{nn'}\] is the orthogonality integral. [answer]

First of all, there should be no dependence on \(\theta\), because the piston is positioned on-axis. Thus \(m=0\), and the general solution is \begin{align*} p(r,z,t) &= \sum_{n} A_n J_0(k_rr) e^{j(\omega t - k_zz)} \end{align*} Since \(\partial p/\partial r = 0\) at \(r=a\), \begin{align*} J'_0(k_r a) = 0 \quad \implies \quad k_r = \alpha'_{0n}/a\,. \end{align*} Thus, \(k_z = \beta_n = \sqrt{(\omega/c_0)^2- (\alpha'_{0n}/a)^2}\). Meanwhile, to satisfy the boundary condition at \(z = 0\), the momentum equation is invoked and set equal to the boundary condition: \begin{align} u^{(z)} &= -\frac{1}{j\omega \rho_0} \frac{\partial p}{\partial z}\notag\\ &= \frac{1}{\rho_0 c_0}\frac{\beta_n}{k}\sum_{n} A_n J_0(\alpha'_{0n} r/a) e^{j{\omega t}}= \begin{cases} u_0 e^{j\omega t},\quad &r\in [0,b]\\ 0,\quad & r\in (b,a] \end{cases}\,.\tag{i}\label{sldfkjlkjkljlk} \end{align} The orthogonality of the Bessel functions is used to find the expansion coefficient \(A_n\). Letting \(x = r/a\) and thus \(dx = dr/a\), the orthogonality integral becomes \[\int_0^a J_m(\alpha'_{mn} r/a)J_m(\alpha'_{mn'} r/a) r\, dr = \frac{a^2}{2}[1-(m/\alpha'_{mn})^2] J^2_m(\alpha'_{mn'}x) \delta_{nn'}\,,\] which for \(m=0\) reads \[\int_0^a J_0(\alpha'_{0n} r/a)J_0(\alpha'_{0n'} r/a) r\, dr = \frac{a^2}{2} J^2_0(\alpha'_{0n'}) \delta_{nn'} \,.\] Multiplying both sides of equation (\ref{sldfkjlkjkljlk}) by \(J_0(\alpha'_{0n'} r/a) r dr\) gives \begin{align*} \frac{1}{\rho_0 c_0 k}\sum_{n} \beta_n A_n J_0(\alpha'_{0n} r/a)J_0(\alpha'_{0n'} r/a) r dr = \begin{cases} u_0 J_0(\alpha'_{0n'} r/a) r dr,\quad &r\in [0,b]\\ 0,\quad & r\in (b,a] \end{cases} \end{align*} Integrate from \(0\) to \(a\): \begin{align*} \frac{1}{\rho_0 c_0 k}\sum_{n} \beta_n A_n \int_{0}^{a} J_0(\alpha'_{0n} r/a)J_0(\alpha'_{0n'} r/a) r dr &= \begin{cases} u_0 \int_{0}^{a} J_0(\alpha'_{0n'} r/a) r dr,\quad &r\in [0,b]\\ 0,\quad & r\in (b,a] \end{cases}\\ \frac{1}{\rho_0 c_0 k}\sum_{n} \beta_n A_n \int_{0}^{a} J_0(\alpha'_{0n} r/a)J_0(\alpha'_{0n'} r/a) r dr &= u_0 \int_{0}^{b} J_0(\alpha'_{0n'} r/a) r dr\end{align*} The orthogonality relation above for \(m=0\) is used to integrate the left-hand side, and the recursion relation given by equation (11-A-24c) in Blackstock's book is used to integrate the right-hand side: \begin{align*} \frac{a^2}{\rho_0 c_0 k}\sum_{n} \beta_n A_n \frac{1}{2} J_0^2(\alpha'_{0n'}) \delta_{nn'} &= u_0 ({a}/{\alpha'_{0n'}})^2 v J_1(v)\bigg\rvert_{v=0}^{v=\alpha'_{0n'}b/a}\\ \frac{a^2}{2\rho_0 c_0} \frac{\beta_n}{k} A_n J_0^2(\alpha'_{0n}) &=u_0 ab \frac{1}{\alpha_{0n}'} J_1(\alpha'_{0n}b/a)\, \end{align*} Solve for \(A_n\): \begin{align*} A_n = \rho_0 c_0 u_0 \, \frac{b}{a}\, \frac{2k}{\beta_n\alpha_{0n}'}\, \frac{J_1(\alpha'_{0n}b/a)}{[J_0(\alpha'_{0n})]^2 }\,. \end{align*}

For more on this problem, see here.
☸ Write the spinning mode eigenfunction of the wave equation that has a spiral wavefront. What is the relationship between a spinning mode and a vortex beam? What is the equation for surfaces of constant phase? What is the angular velocity of each mode? What is \(m\) called? [answer]

This is an unlikely question because it has to do with my research. The spinning mode eigenfunctions are \[p_{mn} = A_{mn} J_m(\alpha'_{mn}r/a) e^{j(\omega t - \beta_{mn} z \pm m\theta)}\,.\] In general, a beam refers to the radiation of sound in free space subject to diffraction (see the next section). However, it is possible (theoretically, at least) to consider a beam in free space that does not diffract (although its source condition spans the entire source plane, and although it requires an infinite amount of energy to produce. Such a non-diffracting beam simply consists of an eigenmode of the wave equation, i.e., products of Bessel functions in \(r\) and harmonic functions in \(\theta\) and \(z\). As such, these beams are called Bessel beams. They are attractive to researchers because they remove diffraction from problems and greatly simplify analysis, given the fact that Bessel functions have been studied extensively.

The relationship between a spinning mode in a waveguide and a Bessel vortex beam is that they have identical mathematical descriptions, though the spinning mode in a waveguide is subject to radial boundary conditions while a vortex beam is unconstrained in \(r\).

The surface of constant phase is given by \[\omega t - \beta_{mn} z \pm m\theta = \text const.\] At a given \(z\), the differential expression is \(\omega dt \pm m d\theta\), and thus the angular velocity of the \(m^\text{th}\) mode is \[\frac{d\theta}{dt} = -\omega/m.\]
☸ Provide a physical interpretation for the phase speed, cutoff frequency, and group speed in a waveguide. Hint: It is easiest to think of a two-dimensional waveguide for this discussion. [answer]

Think of rectangular drumhead that is clamped at \(y=0\) and \(y=d\), and that is infinite in the \(x\) direction. Let \(\theta_i\) be the angle of an incident ray, and let the wavelength of the incident ray be \(\lambda_i\), as in Blackstock's figure 6.14:

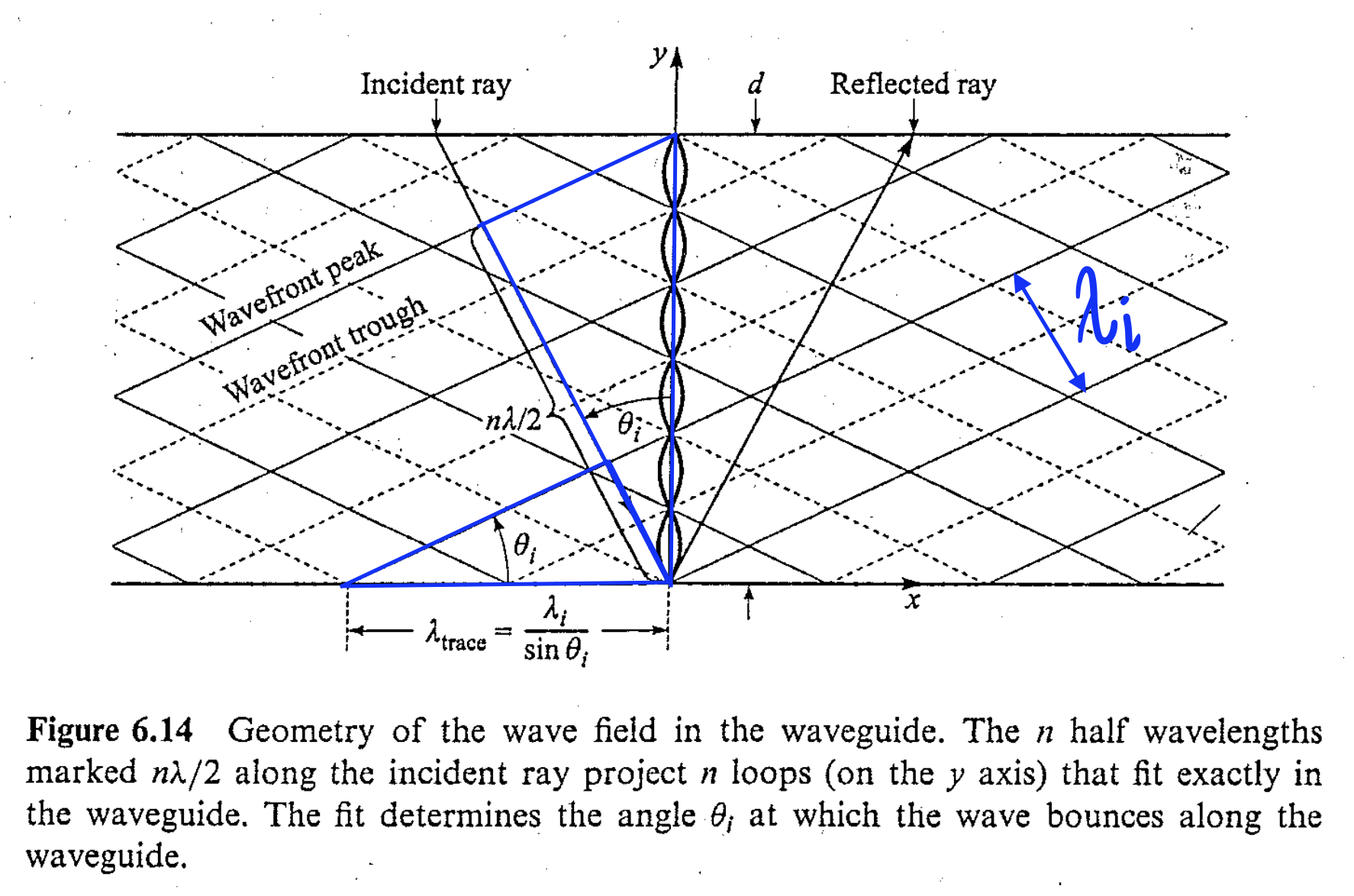
Then, the component of this wavelength on the \(x\) axis is \(\lambda_\text{trace} = \lambda_i/\sin\theta_i\). The speed at which this projection travels is \[c_n^\text{ph} = f\lambda_\text{trace} = \frac{f\lambda}{\sin\theta_i} = \frac{c}{\sin\theta_i} = \frac{c}{\sqrt{1-\cos^2\theta_i}}.\] The superposition of the incident and refleted wave creates a vertical standing wave pattern that has \(n\) loops. From geometry, the \(n\) loops have a projection of \(n\lambda/2\) wavelengths on the incident ray. That is, \(\cos\theta_i = n\lambda/2d = nc/2fd.\) Thus the phase velocity is \[c_n^\text{ph} = \frac{c}{\sqrt{1-(nc/2fd)^2}}.\]

Therefore, for a given \(n\), as the wavelength is increased, \(\theta_i\) becomes smaller and smaller so as to maintain that \(n\) loops are fit about the \(y\) axis. (Think about that limit by making the distance between crests larger. Then the fact that \(\theta_i\) decreases to maintain the location of the nodes will be clear).

As \(\theta_i\) approaches \(0\), lines of constant phase sweep the entire \(x\) axis, and thus the phase speed goes to \(\infty\). (Qualitatively, this makes sense, because lines of constant phase will reach \(x = \pm \infty\) instantaneously; quantitatively this can be seen from the fact that \(c_n^\text{ph} = {c}/{\sin\theta_i}\)). The wavelength for which \(\theta_i = 0\) corresponds to the cutoff frequency. Below this frequency, the sound cannot fit the same \(n\) loops in the vertical direction. Therefore, the sound just cannot live with itself. It kills itself off as an evanescent wave.

Meanwhile, the physical meaning of the group speed is the projection of the wave velocity along the principal axis of the waveguide: \(c^\text{ph}_n = c\sin\theta_i\).
In what frequency limit does the phase speed \(c_\text{ph}\) in a waveguide appoach the speed of sound in free space, \(c\)? [answer]

In the high-frequency limit, the phase speed approaches the free-space sound speed. This is because at high frequencies, a standing wave of very high spatial frequency (large \(k\), small \(\lambda\)) exists in the direction perpendicular to the primary axis of the waveguide. To create this interference pattern, the difference between the trace wavelength and the incident wavelength must be small, and thus \(\theta_i\) must be close to \(90^\circ\) (see figure 6.14 from Blackstock in the answer to the previous question). For \(\theta_i \sim 90^\circ\), the incident sound must be predominantly traveling (as opposed to standing). In the limit that the incident wave is purely traveling, the lines of constant phase travel at the speed of the wavefronts along the axis of the waveguide, and thus \(c_\text{ph} = c\).
What is the phase speed at a cutoff frequency? [answer]

At a cutoff frequency, the phase speed is infinite. This is because at cutoff, the sound has no traveling wave component; rather, the sound is purely a standing wave perpendicular to the waveguide's primary axis. In this standing wave, the lines of constant phase extend infinitely along the waveguide's primary axis. The speed at which lines (in 2D, or surfaces in 3D) of constant phase travel is the phase speed. Since these lines travel an infinite distance in zero time, the phase speed is infinite at a cutoff frequency.

Chapters 13-14: Diffraction

This section is almost entirely based on my class notes from Dr. Hamilton's Acoustics II course. The derivations are challenging, so hints/outlines have been provided. It is more important to understand the underlying concepts.

How does the quantity \(R = |\vec{r}- \vec{r}_0|\) relate a sound source to the listener? [answer]

If the source is located at \(\vec{r}_0\) and the listener is located at \(\vec{r}\), \(R = |\vec{r}- \vec{r}_0|\) is the distance between source and listener. Its shorthand when appearing in the argument of a Green's function is \(\vec{r}|\vec{r}_0\).
☸ Prove that the free space Green's function \(g = e^{-jkR}/4\pi R\) solves the inhomogeneous Helmholtz equation \((\nabla^2 + k^2)f = -\delta(\vec{r} - \vec{r}_0)\), where \(R = |\vec{r}- \vec{r}_0|\). Hint: Integrate the differential equation over the volume and use the divergence theorem. Let the upper radial integration limit be \(\epsilon\), and take the limit as \(\epsilon \to 0\). Also note that \(\int_0^\epsilon e^{-jkR} R dR \to 0 \text{ as } \epsilon \to 0\). [answer]

Inserting the Green's function into the Helmholtz equation and integrating over space gives \begin{align*} \int \nabla^2 g dV + k^2 \int g \, dV &= -1 \end{align*} The divergence theorem is applied to the first integral: \begin{align*} \int \nabla^2 g dV &= \int \gradient\cdot(\gradient g) dV\\ &= \oint \gradient g\, dS \\ &= 4\pi R^2 \frac{d}{dR}\bigg(\frac{e^{-jkR}}{4\pi R}\bigg)\bigg\rvert_{R=0}^{R=\epsilon}\\ &= 4\pi R^2 \bigg(-\frac{1}{4\pi R^2} - \frac{jk}{4\pi R}\bigg)e^{-jkR}\bigg\rvert_{R=0}^{R=\epsilon}\\ &= -(1 + jkR)\, e^{-jkR}\big\rvert_{R=0}^{R=\epsilon}\\ &= -(1 + jk\epsilon)\, e^{-jk\epsilon} \end{align*} Now the limit of the above result is taken: \begin{align*} -\lim_{\epsilon\to 0} (1 + jk\epsilon)e^{-jk\epsilon} &= -\lim_{\epsilon\to 0} (1 + jk\epsilon)(1 - jk\epsilon -k^2\epsilon^2/2! \dots)\\ &=-1\,. \end{align*} Meanwhile, the second integral is \begin{align*} \int \frac{e^{-jkR}}{4\pi R} dV &= \int_0^\epsilon \frac{e^{-jkR}}{4\pi R} 4\pi R^2 dR\\ &= \int_0^\epsilon e^{-jkR} R dR \to 0 \text{ as } \epsilon \to 0\,. \end{align*} Thus one obtains the true statement, \(-1 = -1\). The free space Green's function thus satisfies the inhomogeneous Helmholtz equation.
What is reciprocity in acoustics? [answer]

Reciprocity is the invariance under the exchange of sound source and listener. That is to say, the listener perceives the same sound when exchanging locations with the source of that sound.
To determine the condition that makes a medium reciprocal, suppose there are point sources at positions \(\vec{r}_1\) and \(\vec{r}_2\). The free space Green's functions \(G(\vec{r}|\vec{r}_1)\) and \(G(\vec{r}|\vec{r}_2)\) satisfy their respective inhomogeneous Helmholtz equations. Combination of the Helmholtz equations, integration over volume, and application of the divergence theorem leads to \begin{align}\label{vanishitofffthat}\tag{13} \int_{\mathcal{S}} \bigg[G(\vec{r}|\vec{r}_2) \frac{\partial G(\vec{r}|\vec{r}_1)}{\partial n} - G(\vec{r}|\vec{r}_1) \frac{\partial G(\vec{r}|\vec{r}_2)}{\partial n}\bigg] dS &= G(\vec{r}_2|\vec{r}_1) - G(\vec{r}_1|\vec{r}_2)\,. \end{align} Why does the right-hand side of equation (\ref{vanishitofffthat}) equal \(0\)? What are the three conditions on the boundary of surface \(\mathcal{S}\) in which the left-hand side vanishes, thereby satisfying the equality and giving the conditions for a reciprocal medium? [answer]

The right-hand side of equation (\ref{vanishitofffthat}) equals \(0\) because the free space Green's function is even in the quantity \(\vec{r}_2 - \vec{r}_1\).

The left-hand side vanishes for \begin{align} G &= 0 \label{Greenboundary1}\tag{i}\\ \frac{\partial G}{\partial n} &= 0 \label{Greenboundary2}\tag{ii}\\ \frac{\partial G/\partial n}{G} &= \text{ constant}\,. \label{Greenboundary3}\tag{iii} \end{align} Boundary condition (\ref{Greenboundary1}) corresponds to a pressure release surface; (\ref{Greenboundary2}) corresponds to a rigid surface; and (\ref{Greenboundary3}) corresponds to the Sommerfeld radiation condition or a locally reacting surface.
☸ Starting with the Helmholtz equation for a point-inhomogeneity,\(\nabla^2 G + k^2 G = -\delta(\vec{r} - \vec{r}_0)\), and for a function-inhomogeneity, \(\nabla^2 p + k^2 p = -f(\vec{r})\), derive the Helmholtz-Kirchhoff integral, \begin{align}\label{HKint}\tag{14} p(\vec{r}) = \int_{\mathcal{V}} f(\vec{r}_0) G(\vec{r}|\vec{r}_0)dV_0 + \oint_\mathcal{S} \bigg[G(\vec{r}|\vec{r}_0) \frac{\partial p(\vec{r}_0)}{\partial n_0} - p(\vec{r}_0)\frac{\partial G(\vec{r}|\vec{r}_0)}{\partial n_0} \bigg]dS_0 \end{align} Outline: Relate the two PDEs by multiplying the point-inhomogeneity PDE by \(p\) and the function-inhomogeneity PDE by \(G\). Subtract, interchange \(\vec{r}\) and \(\vec{r}_0\), integrate over volume, and apply the divergence theorem. Why does the surface integral vanish in free space? [answer]

Start with \begin{align} \nabla^2 p(\vec{r}) + k^2 p(\vec{r}) &= -f(\vec{r}) \tag{i}\label{1equation}\\ \nabla^2 G(\vec{r}|\vec{r}_0) + k^2 G(\vec{r}|\vec{r}_0) &= -\delta(\vec{r} - \vec{r}_0)\,. \tag{ii}\label{2equation} \end{align} Multiply equation (\ref{1equation}) by \(G\) and equation (\ref{2equation}) by \(p\), and subtract the two equations. The \(k^2\) terms cancel, giving \begin{align*} G(\vec{r}|\vec{r}_0)\nabla^2 p(\vec{r}) - p(\vec{r}) \nabla^2 G(\vec{r}|\vec{r}_0) &= -f(\vec{r}) G(\vec{r}|\vec{r}_0) + \delta(\vec{r} - \vec{r}_0) p(\vec{r}) \end{align*} Next, interchange \(\vec{r}\) and \(\vec{r}_0\) and integrate over volume \(V_0\). Note that \(G\) cares not about this exchange, nor does the delta function. \begin{align*} \int_{\mathcal{V}} [G(\vec{r}|\vec{r}_0)\nabla^2_0 p(\vec{r}_0) - p(\vec{r}_0) \nabla^2_0 G(\vec{r}|\vec{r}_0)] dV_0 &= \int_{\mathcal{V}} [\delta(\vec{r} - \vec{r}_0) p(\vec{r}_0)-f(\vec{r}_0) G(\vec{r}|\vec{r}_0) ] dV_0\\ &= p(\vec{r}) - \int_{\mathcal{V}}f(\vec{r}_0) G(\vec{r}|\vec{r}_0) ] dV_0\,. \end{align*} Finally, using the divergence theorem on the left-hand side above reduces the Laplacian operators to derivatives on the normal. Solving for \(p(\vec{r})\) results in the Helmholtz-Kirchhoff integral: \[p(\vec{r}) = \int_{\mathcal{V}} f(\vec{r}_0) G(\vec{r}|\vec{r}_0)dV_0 + \int_\mathcal{S} \bigg[G(\vec{r}|\vec{r}_0) \frac{\partial p(\vec{r}_0)}{\partial n_0} - p(\vec{r}_0)\frac{\partial G(\vec{r}|\vec{r}_0)}{\partial n_0} \bigg]dS\]

If the medium is reciprocal, the surface integral vanishes in free space because \(p = 0\) at \(r= \infty\), giving the pressure due to a distribution of sources in free space: \[p(\vec{r}) = \int_{\mathcal{V}} f(\vec{r}_0) G(\vec{r}|\vec{r}_0)dV_0 \]
☸ Use equation (\ref{HKint}) to derive the Rayleigh integral of the first kind, \begin{align}\label{Rayleigh integral}\tag{15} p(\vec{r}) &= \frac{j\omega \rho_0}{2\pi}\oint_\mathcal{S} \frac{e^{-jkR}}{R} u^{(z)}(\vec{r}_0) dS_0 \end{align} which gives the pressure field due to a velocity source. Let \(\vec{e}_{n0}\) be the unit outward normal, and align the surface source in the plane \(z=0\), as shown below. 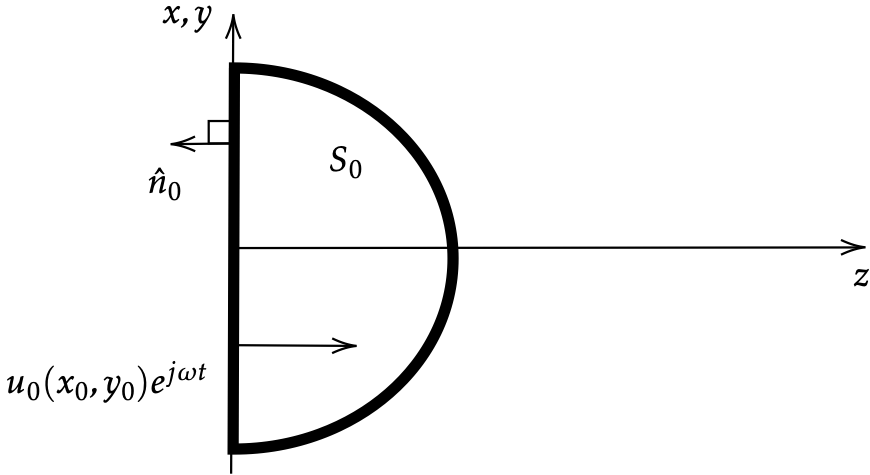Outline: Let the first integral in equation (\ref{HKint}) be zero, i.e., assume no sources distributed in the volume. With the remaining surface integral, write \(\partial p(\vec{r}_0)/\partial n_0 = -\partial p(\vec{r}_0)/\partial z_0\) in terms of particle velocity using the momentum equation. With the second term, choose \(G\) such that \(\partial G/\partial n_0 = 0\) on the surface. The correct choice (show this) is \(G(\vec{r}|\vec{r}_0) = g_+(\vec{r}|\vec{r}_0) + g_-(\vec{r}|\vec{r}_0)\), where \(g_\pm = e^{-jkR_\pm}/4\pi R_\pm\), where \(R_\pm = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z\mp z_0)^2}\). [answer]

Let the first integral in equation (\ref{HKint}) be zero, i.e., assume no sources are distributed in the volume: \begin{align} p(\vec{r}) &= \oint_\mathcal{S} \bigg[G(\vec{r}|\vec{r}_0) \frac{\partial p(\vec{r}_0)}{\partial n_0} - p(\vec{r}_0)\frac{\partial G(\vec{r}|\vec{r}_0)}{\partial n_0} \bigg]dS_0\notag\\ &= \oint_\mathcal{S} \bigg[-G(\vec{r}|\vec{r}_0) \frac{\partial p(\vec{r}_0)}{\partial z_0} + p(\vec{r}_0)\frac{\partial G(\vec{r}|\vec{r}_0)}{\partial z_0} \bigg]\bigg\rvert_{z_0=0}dS_0\label{HKint1}\tag{i} \end{align} Since an equation that maps particle velocity to pressure is desired, write \(\partial p(\vec{r}_0)/\partial n_0\) in terms of particle velocity using the momentum equation. \begin{align*} \frac{\partial p(\vec{r}_0)}{\partial n_0} = -\frac{\partial p(\vec{r}_0)}{\partial z_0} = j\omega \rho_0 u^{(n)}(\vec{r}_0) \end{align*} Next, choosing \(G(\vec{r}|\vec{r}_0) = g_+(\vec{r}|\vec{r}_0) + g_-(\vec{r}|\vec{r}_0)\), where \(g_\pm = e^{-jkR_\pm}/4\pi R_\pm\), where \[R_\pm = \sqrt{(x-x_0)^2 + (y-y_0)^2 + (z\mp z_0)^2},\] note that \begin{align*} \frac{\partial G}{\partial z_0}\bigg\rvert_{z_0=0}&= \frac{\partial g_+}{\partial z_0}\bigg\rvert_{z_0=0} + \frac{\partial g_-}{\partial z_0}\bigg\rvert_{z_0=0}\\ &=\frac{\partial }{\partial z_0}\frac{e^{-jkR_+}}{4\pi R_+}\bigg\rvert_{z_0=0} + \frac{\partial}{\partial z_0}\frac{e^{-jkR_-}}{4\pi R_-}\bigg\rvert_{z_0=0}\\ &=\bigg[\frac{jke^{-jkR_+}(z-z_0)}{4\pi R_+^2} + \frac{(z-z_0)}{4\pi R_+^3}e^{-jkR_+} -\frac{jke^{-jkR_-}(z+z_0)}{4\pi R_-^2} - \frac{(z+z_0)}{4\pi R_-^3}e^{-jkR_-} \bigg]_{z=0} \end{align*} Note that for \(z_0=0\), \(R_+ = R_-\equiv R\), and the above equation becomes \begin{align} \frac{\partial G}{\partial z_0}\bigg\rvert_{z_0=0}&=\frac{jke^{-jkR}(z-z_0)}{4\pi R^2} + \frac{(z-z_0)}{4\pi R^3}e^{-jkR} -\frac{jke^{-jkR}(z+z_0)}{4\pi R^2} - \frac{(z+z_0)}{4\pi R^3}e^{-jkR}\notag\\ &=0\tag*{woohoo!} \end{align} Also, \(g_+ = g_- \equiv g\) at \(z_0=0\), so \(G = 2g = e^{-jkR/4\pi R}\). So equation (\ref{HKint1}) becomes \begin{align*} p(\vec{r}) &= \oint_\mathcal{S} \bigg(\frac{2e^{-jkR}}{4\pi R}\bigg) \big[j\omega \rho_0 u^{(r)}\big] dS_0 \end{align*} Rearranging gives the famous Rayleigh integral of the first kind of acoustics (and the second kind of optics): \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0}{2\pi}\oint_\mathcal{S} \frac{e^{-jkR}}{R} u^{(r)}(\vec{r}_0) dS_0 \end{align*} In Cartesian coordinates, \begin{align*} p(x,y,z) &= \frac{j\omega \rho_0}{2\pi}\iint_{-\infty}^\infty \frac{e^{-jkR}}{R} \, u^{(r)}(x_0,y_0,0) \,dx_0\, dy_0\,. \end{align*} where \(R = \sqrt{(x-x_0)^2 + (y-y_0)^2 +z^2}\). Note that the contour integral symbol \(\oint\) denoting "integral over a closed surface" is abandoned because there is no sound incident on the surface infinitely far away. (This relates to the Sommerfeld radiation condition).
Use the Rayleigh integral for a velocity source, Eq. (\ref{Rayleigh integral}) to calculate the on-axis (\(x=y=0\)) field due to a uniform circular piston of radius \(a\). [answer]

Setting \(x = y =0\) in Cartesian coordinates corresponds to setting \(\sigma=0\) in cylindrical coordinates in the Rayleigh integral, Eq. (\ref{Rayleigh integral}), and thus \(R = \sqrt{\sigma_0^2 + z^2}\). Also, since the field is axisymmetric, \(u^{(z)}(\vec{r}_0) = u^{(z)}(\sigma_0)\). Eq. (\ref{Rayleigh integral}) therefore becomes \begin{align*} p(0,z) &= \frac{j\omega \rho_0}{2\pi}\int_{0}^{2\pi}\!\! \int_{0}^{\infty} \frac{e^{-jkR}}{R} u^{(z)}(\sigma_0) \sigma_0 d\sigma_0 d\theta \\ &= \frac{jk\rho_0c_0u_0}{2\pi}\int_{0}^{2\pi}\!\! \int_{0}^{a} \frac{e^{-jk\sqrt{\sigma_0^2 + z^2}}}{\sqrt{\sigma_0^2 + z^2}} \sigma_0 d\sigma_0 d\theta\,. \end{align*} The radial integral contains no \(\theta\) dependence. Thus \begin{align*} p(0,z) &= jk\rho_0c_0u_0\int_{0}^{a} \frac{e^{-jk\sqrt{\sigma_0^2 + z^2}}}{\sqrt{\sigma_0^2 + z^2}} \sigma_0 d\sigma_0 \,. \end{align*} Letting \(s = \sqrt{\sigma_0^2 + z^2}\) and thus \(ds = \sigma_0 d\sigma_0/\sqrt{\sigma_0^2 + z^2}\), the radial integral is evaluated: \begin{align*} p(0,z) &= jk\rho_0c_0u_0\int_{z}^{\sqrt{a^2 + z^2}} e^{-jks} ds \\ &= -\rho_0c_0 u_0 \exp(-jks)\bigg\rvert_{z}^{\sqrt{a^2+z^2}}\\ &= \rho_0c_0 u_0 [\exp(-jkz) - \exp(-jk\sqrt{a^2+z^2})]\,. \end{align*} The above can be factorized as \begin{align*} p(0,z) &= \rho_0c_0 u_0 \exp\bigg[\frac{jk}{2}(-z - \sqrt{a^2+z^2})\bigg] \bigg\lbrace\exp\bigg[\frac{jk}{2}(-z + \sqrt{a^2+z^2})\bigg] - \exp\bigg[\frac{jk}{2}(z - \sqrt{a^2+z^2})\bigg]\bigg\rbrace\,. \end{align*} Recalling that \((e^{jx}-e^{-jx})/2j = \sin x\), the above becomes \begin{align*} p(0,z) &= 2j\rho_0c_0 u_0 \exp[-jk(z + \sqrt{a^2+z^2})/2] \sin[k(\sqrt{a^2+z^2} - z)/2] \,. \end{align*} The magnitude of this expression is \begin{align*} |p(0,z)| &= 2\rho_0c_0 u_0 \big|\sin[k(\sqrt{a^2+z^2}-z)/2]\big| \,. \end{align*}
☸ Derive the Rayleigh integral of the second kind, \begin{align}\label{Rayleigh integral 2}\tag{16} p(\vec{r}) &= \frac{jkz}{2\pi} \oint p(\vec{r}_0) \bigg(1 + \frac{1}{jkR} \bigg) \frac{e^{-jkR}}{R^2} dS_0\,, \end{align} which gives the pressure field due to a pressure source. Start with equation (\ref{HKint}), and follow the derivation for the first Rayleigh integral, only now choosing \(G(\vec{r}|\vec{r}_0) = g_+(\vec{r}|\vec{r}_0) - g_-(\vec{r}|\vec{r}_0)\). What is this integral called in optics? [answer]

As in the derivation of the first Rayleigh integral, let the first integral in equation (\ref{HKint}) be zero, i.e., assume no sources are distributed in the volume. Since an equation that maps pressure to pressure is desired, it is desired for \(\partial G(\vec{r}|\vec{r}_0)/\partial n_0\) to vanish on the boundary. Choosing \(G(\vec{r}|\vec{r}_0) = g_+(\vec{r}|\vec{r}_0) - g_-(\vec{r}|\vec{r}_0)\) does the trick, because at the \(z=0\), \(R_+ = R_- \equiv R\), and thus \(g_+ = g_- \equiv g\), so \begin{align*} G(\vec{r}|\vec{r}_0)\bigg\rvert_{z_0=0} = g(\vec{r}|\vec{r}_0) - g(\vec{r}|\vec{r}_0)= 0\,. \end{align*} Thus the Helmholtz-Kirchhoff integral becomes \begin{align} p(\vec{r}) &= \oint_\mathcal{S} p(\vec{r}_0)\frac{\partial G(\vec{r}|\vec{r}_0)}{\partial z_0}\bigg\rvert_{z_0=0} dS_0\notag\\ &= \oint p(x_0,y_0,0) \bigg[\frac{\partial }{\partial z_0}\frac{e^{-jkR_+}}{4\pi R_+} - \frac{\partial}{\partial z_0}\frac{e^{-jkR_-}}{4\pi R_-}\bigg] \bigg\rvert_{z_0=0} dx_0dy_0\tag{ii}\label{suberherslkdf} \end{align} Note that the term in the square brackets is evaluated separately to be \begin{align*} \bigg[\dots\bigg]&=\bigg[\frac{jke^{-jkR_+}(z-z_0)}{4\pi R_+^2} + \frac{(z-z_0)}{4\pi R_+^3}e^{-jkR_+} +\frac{jke^{-jkR_-}(z+z_0)}{4\pi R_-^2} + \frac{(z+z_0)}{4\pi R_-^3}e^{-jkR_-} \bigg]_{z_0=0}\\ &= \frac{jke^{-jkR}z}{4\pi R^2} + \frac{z}{4\pi R^3}e^{-jkR} +\frac{jke^{-jkR}z}{4\pi R^2} + \frac{z}{4\pi R^3}e^{-jkR}\\ &= \frac{jke^{-jkR}z}{2\pi R^2} + \frac{z}{2\pi R^3}e^{-jkR}\\ &= \frac{jkz}{2\pi} \bigg(1 + \frac{1}{jkR} \bigg) \frac{e^{-jkR}}{R^2} \end{align*} Thus equation (\ref{suberherslkdf}) becomes \begin{align*} p(\vec{r}) &= \frac{jkz}{2\pi} \oint p(\vec{r}_0) \bigg(1 + \frac{1}{jkR} \bigg) \frac{e^{-jkR}}{R^2} dS_0\,, \end{align*} or in Cartesian coordinates, \begin{align*} p(x,y,z) &= \frac{jkz}{2\pi} \iint_{-\infty}^\infty p(x_0,y_0,0) \bigg(1 + \frac{1}{jkR} \bigg) \frac{e^{-jkR}}{R^2} dx_0dy_0 \end{align*} where \(R=\sqrt{(x-x_0)^2 + (y-y_0)^2 +z^2}\). Again, the contour integral symbol \(\oint\) denoting "integral over a closed surface" is abandoned because there is no sound incident on the surface infinitely far away.

This integral is called the Rayleigh integral of the first kind in optics because (need to confirm) usually in optics the source condition is given in terms of the field variable. That is to say, \(E(x_0,y_0,0)\) is used to compute \(E(x,y,z)\), while or \(H(x_0,y_0,0)\) is used to compute \(H(x,y,z)\).
☸ Obtain the Fraunhofer approximation of the Rayleigh integral of the first kind (\ref{Rayleigh integral}): \begin{align}\label{Fraunhofer}\tag{17} p(\vec{r}) &= \frac{j\omega \rho_0}{2\pi}\frac{e^{-jkr}}{r} \iint_{-\infty}^\infty e^{jk_xx_0 + jk_yy_0} u_0(x_0,y_0) dx_0 dy_0 \end{align} Outline: Expand the squares in the displacement \(R = \sqrt{(x-x_0)^2 + (y-y_0)^2 +z^2},\) identify \(r^2 = x^2+ y^2+z^2\), and take the first-order binomial expansion of \(R\). Multiply by \(k\) to make the quantity dimensionless, and throw out quadratic terms (terms proportional to \(x_0^2,y_0^2\)). Finally, interpret \(k_x \equiv kx/r\) and \(k_y \equiv ky/r\). Do you recognize the resulting 2D integral? At what \(r\) does the Fraunhofer approximation hold? [answer]

Begin by expanding \(R\): \begin{align*} R &= \sqrt{(x-x_0)^2 + (y-y_0)^2 +z^2}\\ &= \big[x^2 + y^2 + z^2 -2xx_0 - 2yy_0 + x_0^2 + y_0^2\big]^{1/2}\\ &= \big[r^2 -2xx_0 - 2yy_0 + x_0^2 + y_0^2\big]^{1/2}\\ &= r \bigg[1 -2 \frac{xx_0 + yy_0}{r^2} + \frac{x_0^2 + y_0^2}{r^2} \bigg]^{1/2}\\ \end{align*} Now perform the binomial expansion to first order: \begin{align*} R&= r \bigg[1 - \frac{xx_0 + yy_0}{r^2} + \frac{x_0^2 + y_0^2}{2r^2}\bigg]\\ &= r - \frac{xx_0 + yy_0}{r} + \frac{x_0^2 + y_0^2}{2r} \,. \end{align*} Next, multiply by \(k\) to make the quantity dimensionless (and because this is the combination that appears in the Rayleigh integral), and toss the term that is quadratic: \begin{align*} kR &= kr - kx_0\frac{x}{r} - ky_0\frac{y}{r}\\ &=kr - k_x x_0 - k_y y_0\,. \end{align*} where the interpretation \(k_x \equiv kx/r\) and \(k_y \equiv ky/r\) has been made. Approximate the amplitude in equation (\ref{Rayleigh integral}) to zeroth order and the phase to linear order: \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0}{2\pi}\frac{e^{-jkr}}{r} \iint_{-\infty}^\infty e^{jk_xx_0 + jk_yy_0} u_0(x_0,y_0) dx_0 dy_0 \end{align*} (Note that the notation changes here from denoting the velocity source condition from \(u^{(r)}\) to \(u_0\)). The integral above is simply the 2D spatial Fourier transform of the source condition. This is often denoted \(\hat{u}(k_x,k_y)\). The directivity is defined as \[D(\theta,\psi) = \frac{\hat{u}_0(k_x,k_y)}{\hat{u}_0(0,0)}.\]

The Fraunhofer approximation holds for \(r \gtrsim 3R_0\), where \(R_0= ka^2/2\), the Rayleigh distance.
What is the \(ka \ll 1\) limit of the Fraunhofer approximation? [answer]

In this limit the exponential in equation (\ref{Fraunhofer}) \(\to 1\). Thus the 2D spatial Fourier transform simply becomes the surface integral over the velocity source condition, which is \(Q_0\), the volume velocity. Thus the \(ka \ll 1\) limit of the Fraunhofer approximation is an acoustic monopole: \[p(\vec{r}) = \frac{j\omega \rho_0 Q_0}{2\pi} \frac{e^{-jkr}}{r}\,.\]
Convert the Fraunhofer approximation, equation (\ref{Fraunhofer}), which is given in terms of rectangular coordinates in the source plane, to polar coordinates in the source plane using the change-of-variables in which \(\kappa = k\sin\theta\), and \begin{alignat*}{2} x&= \sigma \cos \psi \qquad y&&= \sigma \sin \psi \\ k_x&= \kappa\cos \phi \qquad k_y&&= \kappa\sin \phi\,. \end{alignat*} Then simplify the result to the case of an axisymmetric beam (no dependence on \(\psi\)). [answer]

The argument of the exponential in the integrand of equation (\ref{Fraunhofer}) becomes \begin{align*} k_xx_0 + k_yy_0 &= \kappa\cos \phi\,\,\,\sigma_0 \cos \psi_0 \,\,\, + \,\,\, \kappa\sin \phi\,\,\, \sigma_0 \sin \psi_0 \\ &= \kappa\sigma_0 (\cos \phi\,\,\cos \psi_0 \, + \, \sin \phi\,\, \sin \psi_0)\\ &= \kappa\sigma_0 \cos(\phi -\psi_0) \end{align*} Also, \(dx_0\,dy_0 = \sigma_0\, d\sigma_0\, d\psi_0 \). Thus equation (\ref{Fraunhofer}) becomes \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0}{2\pi}\frac{e^{-jkr}}{r} \int_{0}^{2\pi}\int_{0}^{\infty} e^{j\kappa\sigma_0 \cos(\phi -\psi_0)} u_0(\sigma_0,\psi_0) \, \sigma_0\, d\sigma_0 d\psi_0\\ &= \frac{j\omega \rho_0}{2\pi}\frac{e^{-jkr}}{r} \int_{0}^{2\pi} e^{j\kappa\sigma_0 \cos(\phi -\psi_0)} d\psi_0 \int_{0}^{\infty} u_0(\sigma_0)\, \sigma_0\, d\sigma_0 \end{align*} The first line above is the farthest the Fraunhofer approximation can be taken if the source condition has an angular dependence (e.g., a vortex beam). In the second line, it has been assumed that \(u_0 = u_0(\sigma_0)\). In that case, identify \(2\pi\, J_0(\kappa \sigma_0) = \int_{0}^{2\pi} e^{j\kappa\sigma_0 \cos(\phi -\psi_0)} d\psi_0\), i.e., an integral representation of the Bessel function. Thus \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0}{2\pi}\frac{e^{-jkr}}{r} \bigg[2\pi \int_{0}^{\infty} J_0(\kappa \sigma_0) u_0(\sigma_0) \,\sigma_0 \, d\sigma_0 \bigg] \end{align*} The integral above is the Hankel transform, denoted \(\hat{u}_{0,H}(\kappa)\), and the quantity in brackets \([\dots]\) is \(2\pi\, \hat{u}_{0,H}(\kappa)\), which is simply the Fourier transform. Also, note that \(J_0(0) = 1\). Thus the volume velocity is given by \(\hat{u}_{0,H}(0) = Q_0 = 2\pi \int_{0}^{\infty} u_0(\sigma_0) \,\sigma_0 \, d\sigma_0\). Multiplying and dividing by the volume velocity gives \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0 Q_0}{2\pi}\frac{e^{-jkr}}{r} \frac{2\pi \int_{0}^{\infty} J_0(\kappa \sigma_0) u_0(\sigma_0) \,\sigma_0 \, d\sigma_0}{2\pi \int_{0}^{\infty} u_0(\sigma_0) \,\sigma_0 \, d\sigma_0}\\ &=\frac{j\omega \rho_0 Q_0}{2\pi}\frac{e^{-jkr}}{r} \frac{2\pi \int_{0}^{\infty} J_0(\kappa \sigma_0) u_0(\sigma_0) \,\sigma_0 \, d\sigma_0}{\hat{u}_{0,H}(0)} \end{align*} The pressure field is thus written in terms of the directivity \(D(\theta)\): \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0 Q_0}{2\pi}\frac{e^{-jkr}}{r}D(\theta) \\ D(\theta) &= \frac{\hat{u}_{0,H}(\kappa)}{\hat{u}_{0,H}(0)} \end{align*}
Find the far-field pressure field and directivity due to a thin ring of pressure at \(z=0\) centered about the \(z\) axis, given by the condition \begin{align*} u_0(\sigma) = u_0 w \delta(\sigma-a) \end{align*} where \(\sigma\) is the radial coordinate in the source plane. [answer]

Recall from the previous question that the pressure field is given by \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0 Q_0}{2\pi}\frac{e^{-jkr}}{r}D(\theta) \\ D(\theta) &= \frac{\hat{u}_{0,H}(\kappa)}{\hat{u}_{0,H}(0)} \end{align*} where the Hankel transform is defined as \begin{align*} \hat{u}_{0,H}(\kappa) = \int_{0}^{\infty} J_0(\kappa \sigma_0) u_0(\sigma_0) \,\sigma_0 \, d\sigma_0\,. \end{align*} Letting \(u_0(\sigma) = u_0 w \delta(\sigma-a)\), the Hankel transform is calculated using the sifting property of the delta function: \begin{align*} \hat{u}_{0,H}(\kappa) &= u_0 w \, \int_{0}^{\infty} J_0(\kappa \sigma_0) \delta(\sigma-a) \,\sigma_0 \, d\sigma_0\\ &= u_0 w a \, J_0(\kappa a) \end{align*} Thus \(\hat{u}_{0,H}(0) = u_0 w a\). So the far-field directivity is given by \[D(\theta) = J_0(\kappa a) = J_0 (ka\sin\theta)\,,\] and the pressure in the far field is given by \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0 Q_0}{2\pi}\frac{e^{-jkr}}{r} J_0 (ka\sin\theta)\,. \end{align*}
Find the far-field pressure field and directivity due to a uniform circular piston at \(z=0\) centered about the \(z\) axis, given by the condition \begin{align*} u_0(\sigma) = \begin{cases} u_0,\quad \sigma \in [0,a] \\ 0,\quad \sigma > a \end{cases}\,, \end{align*} where \(\sigma\) is defined as before. [answer]

Recall from the previous two questions that the pressure field is given by \begin{align*} p(\vec{r}) &= \frac{j\omega \rho_0 Q_0}{2\pi}\frac{e^{-jkr}}{r}D(\theta) \\ D(\theta) &= \frac{\hat{u}_{0,H}(\kappa)}{\hat{u}_{0,H}(0)} \end{align*} where the Hankel transform is \(\hat{u}_{0,H}(\kappa) = \int_{0}^{\infty} J_0(\kappa \sigma_0) u_0(\sigma_0) \,\sigma_0 \, d\sigma_0\). Letting \(u_0(\sigma) = u_0\) for \(\sigma \in [0,a]\) and \(0\) for \(\sigma > a\), the Hankel transform is calculated: \begin{align*} \hat{u}_{0,H}(\kappa) &= u_0 \, \int_{0}^{a} J_0(\kappa \sigma_0) \,\sigma_0 \, d\sigma_0\\ &= u_0 a^2 \frac{J_1(\kappa a)}{\kappa a}\,. \end{align*} Since \(\lim_{x\to 0} J_1(x)/x = 1/2\), \(\hat{u}_{0,H}(0) = u_0 a^2/2\). So the far-field directivity is given by \[D(\theta) = \frac{2J_1(\kappa a)}{\kappa a} = \frac{2J_1(ka\sin\theta)}{ka\sin\theta} \,,\] and the pressure in the far field is \begin{align*} p(\vec{r}) &= j\rho_0 c_0 u_0 \frac{ka^2}{2}\frac{e^{j(\omega t - kr)}}{r} \frac{2J_1(ka\sin\theta)}{ka\sin\theta}\,. \end{align*}
☸ Obtain the Fresnel (paraxial) approximation of equation (\ref{Rayleigh integral}). The result is \begin{align}\label{Fresnel}\tag{18} p(x,y,z) &= \frac{j\omega \rho_0}{2\pi}\frac{e^{-jkz}}{z}\iint_{-\infty}^\infty \, u_0(x_0,y_0) e^{-jk [(x-x_0)^2 + (y-y_0)^2]/2z}\,dx_0\, dy_0\,. \end{align} Outline: Expand \(R\) in powers of \(1/z\) (whereas in the Fraunhofer approximation, \(R\) was expanded in powers of \(1/r\)). What are the limits on this approximation? [answer]

Start with the first Rayleigh integral, given by equation (\ref{Rayleigh integral}), where \[R = \sqrt{(x-x_0)^2 + (y-y_0)^2 +z^2}\,.\] As in the Fraunhofer approximation, \(R\) is the quantity that is approximated. However, this time it is expanded in powers of \(1/z\): \begin{align*} R &= z\bigg[{1 + \frac{(x-x_0)^2}{z^2} + \frac{(y-y_0)^2}{z^2}}\bigg]^{1/2} \end{align*} The quadratic terms are considered to be small, and the binomial expansion is applied: \begin{align*} R &= z\bigg[{1 + \frac{(x-x_0)^2}{2z^2} + \frac{(y-y_0)^2}{2z^2}}\bigg]\\ &=z + \frac{(x-x_0)^2}{2z} + \frac{(y-y_0)^2}{2z} \end{align*} The denominator of the integrand of equation (\ref{Rayleigh integral}) is approximated to zeroth order as \(z\). Meanwhile, the quantity \(kR\) that appears in the exponent becomes \begin{align*} kR &= kz + \frac{k}{2z}\big[(x-x_0)^2 + (y-y_0)^2\big] \end{align*} Note that the next higher order term would be \(\mathcal{O}(z^{-3}) \sim ka^4/8z^3\) which is declared to be \(\ll \pi\), i.e., the \(\mathcal{O}(z^{-3})\) does not contribute significantly to the phase of \(e^{-jkR}\), giving the criterion for the paraxial approximation to be \((z/a)^3 \gtrsim ka/8\pi\), or simply \(z/a \gtrsim (ka)^{1/3}\), which corresponds to a region defined by a \(\pm 20^\circ\) angle about the \(z\) axis (the paraxial region). Thus the first Rayleigh integral becomes \begin{align*} p(x,y,z) &= \frac{j\omega \rho_0}{2\pi}\frac{e^{-jkz}}{z}\iint_{-\infty}^\infty \, u_0(x_0,y_0) e^{-jk [(x-x_0)^2 + (y-y_0)^2]/2z}\,dx_0\, dy_0\,. \end{align*} where \(u^{(r)}(x_0,y_0,0)\) has been notated \(u_0(x_0,y_0)\) for simplicity. This is known as the "Fresnel diffraction integral." However, it should not be called the "Fresnel integral," which refers to an integral involved in the diffraction of waves about semi-infinite screens or double-rectangular apertures.
Does the paraxial approximation depend on \(ka\)? Does the paraxial approximation contain evanescent waves? [answer]

While the paraxial approximation is entirely independent of \(ka\), an implicit assumption underlying the paraxial approximation is that \(ka \gg 1\). This condition keeps the wavefronts quasi-planar. The "plane wave part" of the Fresnel diffraction integral is the factor \(e^{-ikz}\) in front of the integral.

The paraxial approximation does not contain evanescent waves. This can be seen by noting that the quantity \begin{align*} kR &= kz + \frac{k}{2z}\big[(x-x_0)^2 + (y-y_0)^2\big] \end{align*} is purely real-valued and becomes purely imaginary when multiplied by \(-j\) in the exponential \(e^{-jkR}\). Thus there are only exponentials of imaginary arguments, which correspond to propagating waves. (In contrast, recall that evanescent waves correspond to exponentials of real arguments).
Obtain the axisymmetric form of equation (\ref{Fresnel}), using the rectangular-to-polar mapping \begin{alignat*}{2} x&= \sigma \cos \psi \quad x_0 &&= \sigma_0 \cos\psi_0\\ y&= \sigma \sin \psi \quad y_0 &&= \sigma_0 \sin\psi_0 \end{alignat*} and thus \(dx_0 dy_0 = \sigma_0 d\sigma_0 d\psi_0\). Denote \(\omega \) as \(kc_0\). [answer]

Begin with the rectangular form of the Fresnel diffraction integral, equation (\ref{Fresnel}), only with \(\omega\) denoted as \(kc_0\): \begin{align*} p(x,y,z) &= \frac{jk \rho_0 c_0}{2\pi}\frac{e^{-jkz}}{z}\iint_{-\infty}^\infty \, u_0(x_0,y_0) e^{-jk [(x-x_0)^2 + (y-y_0)^2]/2z}\,dx_0\, dy_0, \end{align*} and note that \begin{align*} (x-x_0)^2 + (y-y_0)^2 &= \sigma^2 \cos^2 \psi + \sigma_0^2 \cos^2\psi_0 - 2\sigma\sigma_0 \cos \psi \cos \psi_0 \\ &\quad + \sigma^2 \sin^2 \psi + \sigma_0^2 \sin^2\psi_0 - 2\sigma\sigma_0 \sin\psi \sin\psi_0\\ &= \sigma^2 + \sigma_0^2 - 2\sigma \sigma_0 (\cos \psi \cos\psi_0 + \sin\psi \sin\psi_0)\\ &= \sigma^2 + \sigma_0^2 - 2\sigma \sigma_0 \cos(\psi -\psi_0) \end{align*} Thus the Fresnel diffraction integral becomes \begin{align*} p(\sigma,\psi,z) &= \frac{jk \rho_0 c_0}{2\pi}\frac{e^{-jkz}}{z}\int_{0}^{2\pi} \int_{0}^\infty \, u_0(\sigma_0,\psi_0) e^{-jk [\sigma^2 + \sigma_0^2 - 2\sigma \sigma_0 \cos(\psi -\psi_0)]/2z}\,\sigma_0\,d\sigma_0\, d\psi_0 \,. \end{align*} This is as far as one can go if \(u_0\) depends on the polar angle \(\psi_0\). If \(u_0\) does not depend on this angle, the above becomes \begin{align*} p(\sigma, \psi, z) &= \frac{jk \rho_0 c_0}{2\pi}\frac{e^{-jkz}}{z}e^{-jk\sigma^2/2z} \int_{0}^\infty u_0(\sigma_0) e^{-jk\sigma_0^2/2z}\sigma_0\,d\sigma_0\, \int_{0}^{2\pi} e^{j(k\sigma \sigma_0/z) \cos(\psi -\psi_0)}\, d\psi_0 \end{align*} The polar integral is an integral representation of the Bessel function. It equals \(2\pi J_0 (k\sigma \sigma_0/z)\). Thus \begin{align}\label{Fresnelaxi}\tag{i} p(\sigma, \psi, z) &= e^{-jkz} \bigg[\frac{jk \rho_0 c_0}{z}e^{-jk\sigma^2/2z} \int_{0}^\infty u_0(\sigma_0) J_0 (k\sigma \sigma_0/z) e^{-jk\sigma_0^2/2z}\sigma_0\,d\sigma_0\bigg]\,. \end{align} Note that equation (\ref{Fresnelaxi}) is of the form \(p = q e^{-jkz}\), where \(q\) is the quantity in \([\dots]\) above. This \(q\) is the quantity that is slowly varying in \(z\), and \(e^{-jkz}\) is simply the plane wave propagator.
How does one include spherical focusing in the Fresnel approximation? Let the focal length be \(d\). Then a spherical wavefront is proportional to \(e^{jk\sqrt{x^2 + y^2 + (z-d)^2}}/\sqrt{x^2 + y^2 + (z-d)^2}\). Let the aperture \(a/d\) be small, where \(a\) is the source radius. [answer]

Start with the spherical wave condition at \(z=0\), the source: \(e^{jk\sqrt{x^2 + y^2 + d^2}}/\sqrt{x^2 + y^2 + d^2}\). Then phase is \begin{align*} jk[x^2 + y^2 + d^2]^{1/2} &= jkd\bigg[ 1 + \frac{x^2 + y^2}{d^2} \bigg]^{1/2}\\ &\simeq jkd + jk\frac{x^2 + y^2}{2d}\,, \end{align*} and the magnitude is simply \begin{align*} [x^2 + y^2 + d^2]^{-1/2} &= \frac{1}{d}[1 + (x^2 + y^2)/d^2]^{-1/2}\simeq \frac{1}{d} \end{align*} Thus focused wave is proportional to \(\frac{e^{jkd}}{d} e^{jk(x_0^2+y_0^2)/2d}\) in the Fresnel approximation, and accounting for focusing simply amounts to a multiplication of the Fresnel diffraction integral by \(e^{jk(x_0^2+y_0^2)/2d}\). In polar coordinates, the focusing factor is \(e^{jk\sigma_0^2/2d}.\) That is, the Fresnel diffraction integral becomes \begin{align*} p(\sigma,\psi,z) &= \frac{jk \rho_0 c_0}{2\pi}\frac{e^{-jkz}}{z}\int_{0}^{2\pi} \int_{0}^\infty \, u_0(\sigma_0,\psi_0) e^{jk\sigma_0^2/2d} e^{-jk [\sigma^2 + \sigma_0^2 - 2\sigma \sigma_0 \cos(\psi -\psi_0)]/2z}\,\sigma_0\,d\sigma_0\, d\psi_0\,, \,. \end{align*} or, for an axisymmetric beam, \begin{align*} p(\sigma, \psi, z) &= e^{-jkz} \bigg[\frac{jk \rho_0 c_0}{z}e^{-jk\sigma^2/2z} \int_{0}^\infty u_0(\sigma_0) J_0 (k\sigma \sigma_0/z) e^{jk\sigma_0^2/2d} e^{-jk\sigma_0^2/2z}\sigma_0\,d\sigma_0\bigg]\,. \end{align*}
In the paraxial approximation, the field in the focal plane of a focused source is given by the ________ transform of the source condition in cartesian coordinates and the ________ transform in polar coordinates. Why is this? [answer]

(2D spatial) Fourier; Hankel. This is because at \(z = d\), the factor \(e^{-jk\sigma_0^2/2z}\) equals \(e^{-jk\sigma_0^2/2d}\), which cancels out with the focusing factor \(e^{jk\sigma_0^2/2z}\), leaving \(\int_0^\infty u_0(\sigma_0) J_0(k\sigma \sigma_0/d)\sigma_0 d\sigma_0\) [the Hankel transform of \(u_0(\sigma_0)\)] as the integral in the paraxial approximation. For source conditions that are not axisymmetric, the integral is the 2D spatial Fourier transform of the source condition, though it takes more algebra to show this.
Derive the paraxial wave equation, \[-j2k\frac{\partial q}{\partial z} + \nabla^2_\perp q= 0\,,\] where \(\nabla^2_\perp\) is the transverse Laplacian, \(\partial/\partial x^2 + \partial/\partial y^2\) in Cartesian coordinates. Start with the Helmholtz equation, \(\nabla^2 p + k^2 p = 0\), and let \(p(x,y,z) = q(x,y,z)e^{-jkz}\). Note that \(\partial^2 q/\partial z^2 \ll 1\). [answer]

Take the derivatives of \(p\), and let subscripts indicate partial differentiation with respect to the subscripted variable. By inspection, \begin{align*} \frac{\partial^2 p}{\partial x^2} = q_{xx}e^{-jkz}\quad \text{and}\quad \frac{\partial^2 p}{\partial y^2} = q_{yy}e^{-jkz}\,. \end{align*} Meanwhile, \begin{align*} \frac{\partial p}{\partial z} &= q_z e^{-jkz} -jk q e^{-jkz} = (q_z -jk q)e^{-jkz}\\ \frac{\partial^2 p}{\partial z^2} &= (q_{zz} -jk q_z)e^{-jkz} - jk (q_z -jk q) e^{-jkz}\\ &=(q_{zz} - j2k q_z - k^2 q) e^{-jkz} \end{align*} The Helmholtz equation in Cartesian coordinates, \(p_{xx} + p_{yy} + p_{zz} + k^2 p = 0\), becomes \begin{align*} q_{xx} e^{-jkz} + q_{yy}e^{-jkz} + (q_{zz} - j2k q_z - k^2 q) e^{-jkz} + k^2 q e^{-jkz} &= 0\\ q_{xx} + q_{yy} + (q_{zz} - j2k q_z - k^2 q) + k^2 q &= 0\\ q_{xx} + q_{yy} + q_{zz} - j2k q_z &= 0\,. \end{align*} Noting that \(q_{zz} \) is small (Dr. Hamilton showed this rigorously in class), and denoting \(\partial/\partial x^2 + \partial/\partial y^2 \equiv \nabla^2_\perp\), results in \[-j2k\frac{\partial q}{\partial z} + \nabla^2_\perp q= 0\,.\]
State Babinet's principle. [answer]

Babinet's principle says that "complementary diffracting objects have complementary diffraction patterns" (Blackstock, page 484). For example, the complementary diffracting object of a finite disk of radius \(a\) in free space is a circular aperture of radius \(a\). Babitnet's principle says that the sum of the radiation patterns individually caused by the finite disk and the aperture must be the same as the radiation pattern of the beam in free space.
The \(i(kx-\omega t)\) convention is adopted for this problem. Use the 2D Fourier transform pair \(\hat{f}(k_x,k_y) = \iint_{-\infty}^\infty f(x,y) e^{-i(k_xx+ k_yy)\,dxdy}\) and \({f}(x,y) = (2\pi)^{-2}\iint_{-\infty}^\infty \hat{f}(k_x,k_y) e^{i(k_xx+ k_yy)\,dk_xdk_y}\) to solve the Helmholtz equation in terms of the source condition \(p(x,y,z=0)\). Hint: note that the Fourier transform of the \(n^\mathrm{th}\) derivative of \(f\) with respect to \(x\) is \((ik_x)^n \hat{f}(k_x,k_y)\) (Prove this!), and that the \(n^\mathrm{th}\) derivative of \(f\) with respect to \(y\) is \((ik_y)^n \hat{f}(k_x,k_y)\). Use these relations to reduce the Helmholtz equation to an second-order ordinary differential equation in \(z\). How does the solution change for a velocity source? [answer]

See here for the solution.

Chapter 15: Arrays

Provide the definition of the directivity function \(D(\theta,\psi)\), directivity factor \(D_i\), and directivity index \(\text{DI}\). [answer]

The directivity is defined as \[D(\theta,\psi) = \frac{p(r,\theta,\psi)}{p(r,\theta_m,\psi_m)} = \frac{\hat{u}(k\alpha,k\beta)}{\hat{u}(0,0)},\] where \(\theta_m\) and \(\psi_m\) are the polar and azimuthal angles corresponding the direction of the beam's maximum. Note that \(\alpha = \sin \theta \cos\psi\) and \(\beta = \sin\theta\sin\psi\). The \(z\) axis is aligned such that \(\theta_m =0\).

The directivity factor is \[D_i = \frac{\langle I_\text{max} \rangle }{\langle I_\text{mono} \rangle},\] where \(\langle I_\text{max} \rangle \) is the maximum intensity in the beam (along the \(z\) axis) and \(\langle I_\text{mono} \rangle \) is the intensity at the same distance due to a monopole radiating the same power \(W\).

The directivity index is simply \(\text{DI} = 10 \log_{10} D_i\) (dB).
☸ Derive an expression for the directivity factor \(D_i\) in terms of the directivity function \(D(\theta, \psi)\). Note from the definition of directivity in the previous problem that \[|D(\theta,\psi)|^2 = \frac{\langle I(\theta,\psi) \rangle }{\langle I_\text{max} \rangle }.\] Combine \(\langle I_\text{mono} \rangle = W/4\pi r^2\) and \(W = \oint \langle I(\theta,\psi) \rangle dS\) to eliminate \(W\) and invoke \(\langle I_\text{max} \rangle |D(\theta,\psi)|^2 = \langle I(\theta,\psi) \rangle \). [answer]

Eliminate \(W\): \begin{align*} \langle I_\text{mono} \rangle &= \frac{1}{4\pi r^2} \oint \langle I(\theta,\psi) \rangle \, dS\\ &= \frac{1}{4\pi r^2} \oint \langle I(\theta,\psi) \rangle \, r^2 \,d\Omega\\ &= \frac{1}{4\pi} \oint \langle I(\theta,\psi) \rangle \, d\Omega \end{align*} Invoke \(\langle I(\theta,\psi) \rangle = \langle I_\text{max} \rangle |D(\theta,\psi)|^2\): \begin{align*} \langle I_\text{mono} \rangle &= \frac{1}{4\pi} \oint \langle I_\text{max} \rangle |D(\theta,\psi)|^2 \, d\Omega\\ \langle I_\text{mono} \rangle &= \frac{\langle I_\text{max} \rangle }{4\pi} \oint |D(\theta,\psi)|^2 \, d\Omega \end{align*} Therefore, the directivity factor is \begin{align*} D_i &= \frac{\langle I_\text{max} \rangle }{\langle I_\text{mono} \rangle } = \frac{4\pi}{\oint |D(\theta,\psi)|^2 \, d\Omega} \end{align*}
Calculate the directivity \(D(\theta,\psi)\) due to \[u_0(x,y) = Q_0 [\delta(x-d/2) + \delta(x+d/2)]\delta(y)\] i.e., two in-phase monopoles separated by distance \(d\). [answer]

The directivity is simply given by \begin{align*} D(\theta,\psi) &= \frac{\hat{u}_0(k_x,k_y)}{\hat{u}_0(0,0)} \end{align*} The numerator is evaluated using the sifting property of the \(\delta\) function: \begin{align*} \hat{u}_0(k_x,k_y) &= Q_0 \iint_{-\infty}^\infty [\delta(x-d/2) + \delta(x+d/2)]\delta(y) e^{j(k_xx + k_yy)} dx dy\\ &= Q_0 \int_{-\infty}^{\infty} [\delta(x-d/2) + \delta(x+d/2)] e^{jk_xx} dx \int_{-\infty}^{\infty} \delta(y) e^{jk_yy}dy\\ &= Q_0 (e^{jk_xd/2} + e^{-jk_xd/2}) e^0\\ &=2Q_0 \cos (k_x d/2) \end{align*} Recalling that \(k_x = k\sin\theta\cos\psi\), the numerator is \begin{align*} \hat{u}_0(k_x,k_y) &=2Q_0 \cos [(kd/2)\sin\theta\cos\psi]\,. \end{align*} Meanwhile, the denominator is simply \(\hat{u}_0(k_x,k_y) = 2Q_0\). Thus the directivity is \begin{align*} D(\theta,\psi) &= \cos [(kd/2)\sin\theta\cos\psi]\,. \end{align*} The directivity is plotted below for \(kd\in [0,35]\).
A line array of \(N\) point sources radiates a pressure field given by \[p(r,\theta) = A \frac{e^{-jkr}}{r} \sum_{n=0}^{N-1} e^{jnkd\sin\theta},\] where \(\theta = 0\) points in the direction perpendicular to the line of sources. Given that \[\sum_{n=0}^{N-1} e^{j2n\phi} = \frac{1-e^{j2N\phi}}{1-e^{j2\phi}},\] show that the directivity of the line array is \[D(\theta) = \frac{\sin N\phi}{N \sin\phi},\] where \(\phi = \frac{kd}{2}\sin(\theta) \). Evaluate the result for \(\theta= 0^\circ\). What is this type of radiation called? What is the type of radiation for \(\theta =90^\circ\) called? [answer]

The right-hand side of the given identity is manipulated into the desired form. \begin{align*} \sum_{n=0}^{N-1} e^{jnkd\sin\theta} &= \frac{1-e^{j2N\phi}}{1-e^{j2\phi}}\\ &= \frac{e^{jN\phi}}{e^{j\phi}} \bigg(\frac{e^{-jN\phi}-e^{jN\phi}}{e^{-j\phi}-e^{j\phi}}\bigg)\\ &= \frac{e^{jN\phi}}{e^{j\phi}} \bigg(\frac{e^{jN\phi}-e^{-jN\phi}}{e^{j\phi}-e^{-j\phi}}\bigg)\\ &= e^{j(N-1)\phi} \frac{\sin (N\phi)}{\sin \phi}\\ &= e^{j(N-1)kd\sin(\theta)/2} \frac{\sin [Nkd\sin(\theta)/2]}{\sin [kd\sin(\theta)/2]} \end{align*} The pressure field is therefore \begin{align*} p(r,\theta)= A \frac{e^{-jkr}}{r} e^{j(N-1)kd\sin(\theta)/2} \frac{\sin [Nkd\sin(\theta)/2]}{\sin [kd\sin(\theta)/2]} \end{align*} Meanwhile, plotting reveals that the maximum occurs at \(\theta_m=0\), for which the pressure is \begin{align*} p(r,\theta_m)= A \frac{e^{-jkr}}{r} N \end{align*} The directivity is therefore \begin{align*} D(\theta) = \frac{p(r,\theta)}{p(r,\theta_m)} = \frac{\sin [Nkd\sin(\theta)/2]}{N\sin [kd\sin(\theta)/2]}\,. \end{align*} For \(\theta = 0\), \(D(0) = 1\). This is referred to as ''broadside radiation.'' For \(\theta = 90^\circ\), the radiation is called ''end-fire.''
Obtain the directivity \(D(\theta,\psi)\) for a continuous line array whose source condition is \(u_0(x,y) = u_0 w\delta(y)\) from \(-L/2 \leq x \leq L/2\) and \(0\) otherwise. [answer]

The directivity is calculated using Fourier transforms: \begin{align*} D(\theta,\psi) &= \frac{\hat{u}_0 (k_x,k_y)}{\hat{u}_0 (0,0)}\,. \end{align*} The numerator is given by \begin{align*} \hat{u}_0 (k_x,k_y) &= \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} u_0 w\delta(y) e^{jk_xx}e^{jk_yy} dxdy\\ &=u_0 w \int_{-L/2}^{L/2} e^{jk_xx} dx\\ &=\frac{u_0 w }{jk_x} e^{jk_xx} \bigg\rvert_{-L/2}^{L/2}\\ &=\frac{u_0 w }{jk_x}[e^{jk_xL/2} - e^{-jk_xL/2}]\\ &=\frac{2 u_0 w }{k_x}\sin{k_xL/2}\\ &={u_0 L w }\frac{\sin{k_xL/2}}{k_x L/2} \end{align*} Meanwhile, the denominator is \begin{align*} \hat{u}_0 (0,0) &= u_0 L w\,. \end{align*} Recall that \(k_x = k\sin\theta \cos \psi\). Thus the directivity is \begin{align*} D(\theta,\psi) &= \frac{\hat{u}_0 (k_x,k_y)}{\hat{u}_0 (0,0)}\\ &= \frac{\sin{[(kL/2) \sin\theta \cos \psi]}}{(kL/2) \sin\theta \cos \psi}\,. \end{align*}
Consider a circular piston, whose directivity is given by the jinc fuction, \(D(\theta) = 2J_1(\kappa a)/\kappa a\). The wavenumber is \begin{align*} \kappa &= \sqrt{k_x^2 + k_y^2}\\ k_x &= k\sin\theta \cos\psi\\ k_y &= k\sin\theta \cos\psi \end{align*} Suppose the beam is now steered with \(k_x\) with \(k(\sin \theta \cos\psi - \sin\theta_0)\). What will the new directivity be? [answer]

\[D(\theta) = \frac{2J_1[ka(\sin\theta -\sin\theta_0)]}{ka(\sin\theta -\sin\theta_0)}\].
☸ A distribution of \(N\) velocity sources, each with a source condition of \(u_1(x-x_n,y-y_n)\), has a total source condition of \[u_0(x,y) = \sum_{n=1}^N u_1(x-x_n, y-y_n)\,.\] Prove that the directivity of the distribution is the product of the directivity of each source and the directivity of the array, where the array is treated as a collection of point sources. Hint: write the above source condition in terms of \(\delta\)-function, \[u_0(x,y) = \sum_{n=1}^N \iint_{-\infty}^\infty u_1(x-x_n, y-y_n) \delta(x-x_n)\delta(y-y_n)\, dx\, dy\,,\] and take the 2D Fourier transform. [answer]

The Fourier transform of the velocity source condition \[u_0(x,y) = \sum_{n=1}^N \iint_{-\infty}^\infty u_1(x-x_n, y-y_n) \delta(x-x_n)\delta(y-y_n)\, dx\, dy\] is taken by noting that the Fourier transform of \(\delta(x-x_n)\) is \(e^{jk_xx_n}\), and similarly the Fourier transform of \(\delta(y-y_n)\) is \(e^{jk_yy_n}\): \[\hat{u}_0(k_x,k_y) = \hat{u}_1(k_x,k_y) \sum_{n} e^{j(k_xx_n +k_yy_n)}\,.\] Dividing by \(\hat{u}_0(0,0) = \hat{u}_1(0,0) \sum_n e^{j(0x_n + 0y_n)} = \hat{u}_1(0,0)\) gives the directivity (see problem 1 of this section), \[D(\theta,\psi) = D_1(\theta,\psi)D_A(\theta,\psi)\,.\]
Suppose there are two circular pistons of radius \(a\) separated by a distance \(d\) from each other (center-to-center). What is the directivity of the two pistons? [answer]

The product theorem makes the problem easy. The directivity of each piston is \[D_1(\theta) = \frac{2J_1(ka\sin\theta)}{ka\sin\theta}\] while the directivity for the \(N=2\) line array is \[D_A(\theta, \psi) = \cos[(kd/2) \sin\theta\cos\psi]\,.\] The directivity of the two circular pistons of radius \(a\) separated by a distance \(d\) is thus \[D(\theta,\psi) = \frac{2J_1(ka\sin\theta)}{ka\sin\theta}\cos[(kd/2) \sin\theta\cos\psi]\,. \]